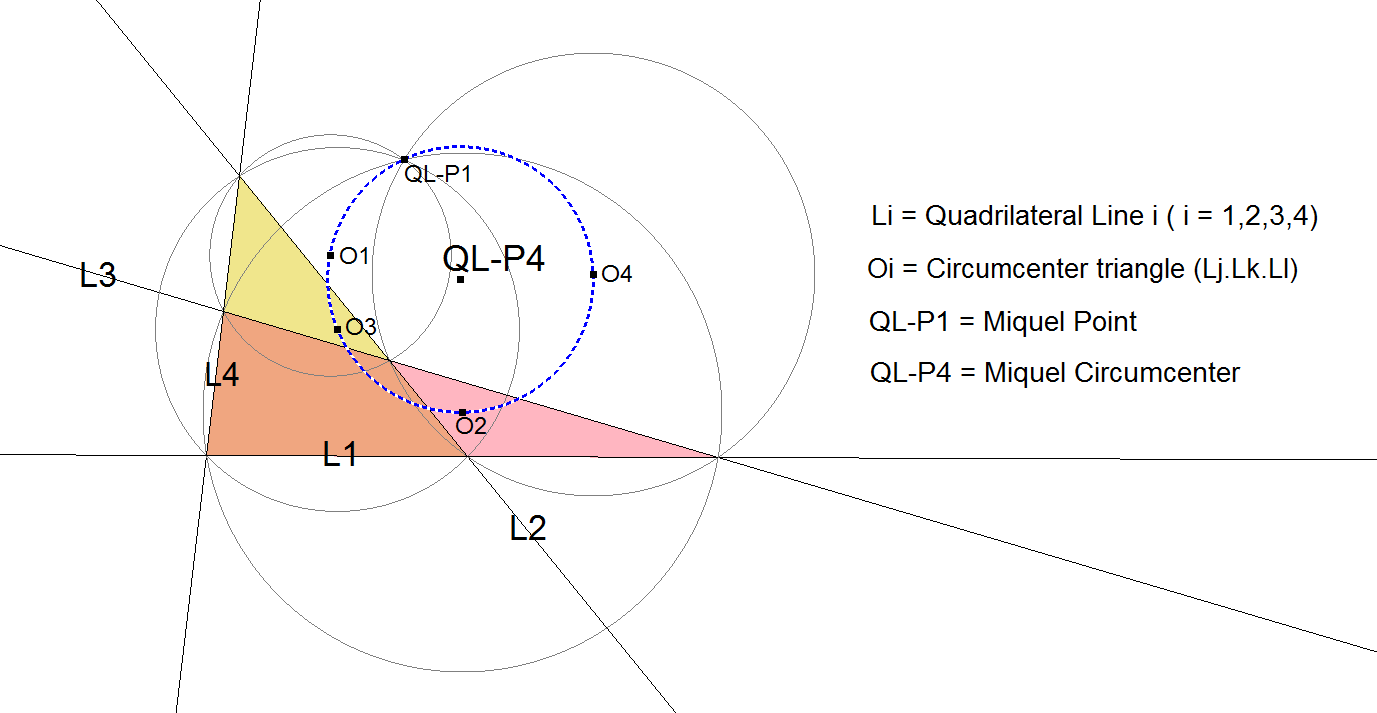
QL-P4: Miquel Circumcenter

The circumcenters of the 4 component triangles of the Reference Quadrilateral are concyclic on the Miquel Circle. It is special that QL-P1, the Miquel Point, also resides on the Miquel Circle. The circumcenter of this circle is QL-P4.

This point is mentioned at [48] and [49] by Morley in resp. 1900 and 1902 as Center of the Center Circle. Morley describes this point as a recursive point for n-Lines.

The point is also mentioned in 1921 by J.W. Clawson (see [31]). He referred to this point as the “center of the circumcentric quadrangle”.

1^st CT-coordinate

a² (a² (m – n) (l – m) (n – l)

+ b² ( l – m) (n² + l m – 2 m n)

+ c² (n – l ) (m² + l n – 2 m n))

1^st DT-coordinate

Sa² (m²-n²)³ – Sb² (l²-n²)² (3 m²+n²) + Sc² (l²-m²)² (m²+3 n²)

+2(m²-n²) (Sa Sc (l²-m²)² + Sa Sb (l²-n²)² – S² (l² (l²+m²+n²)-3 m² n²))

Properties

• QL-P4 lies on these lines:
  • QL-P2.QL-P22        (2 : -1 => QL-P4 = Reflection QL-P2 in QL-P22)
  • QL-P3.QL-P5           (2 : -1 => QL-P4 = Reflection QL-P3 in QL-P5)
• QL-P4 is the Reflection of QL-P5 in QL-P6.
• QL-P4 is the Railway Watcher (see QL-L-1) of QL-L1 (Newton Line) and QL-L4 (Morley Line).
• QL-P4 is the Center of QL-Ci3 (Miquel Circle).
• QL-P4 is the Gergonne-Steiner Point (QA-P3) as well as the Isogonal Conjugate (QA-P4) as well as the Midray Homothetic Center (QA-P8) as well as the QA-DT-Orthocenter (QA-P12) from the Circumcenter Quadrangle (see QL-P3).
• These 4 QA-points concur because the Circumcenter Quadrangle is concyclic.
• The Centroid of the 8 centers of circles as described in rule (9) from Steiner (seen as a system of 8 random points) is QL-P4 (Miquel Circumcenter). See QL-8P1.
• The QA-Möbius Conjugate (QA-Tf4) of QL-P4 is a point on the line QA-P4.QG-P9.

Estimated human page views: 555