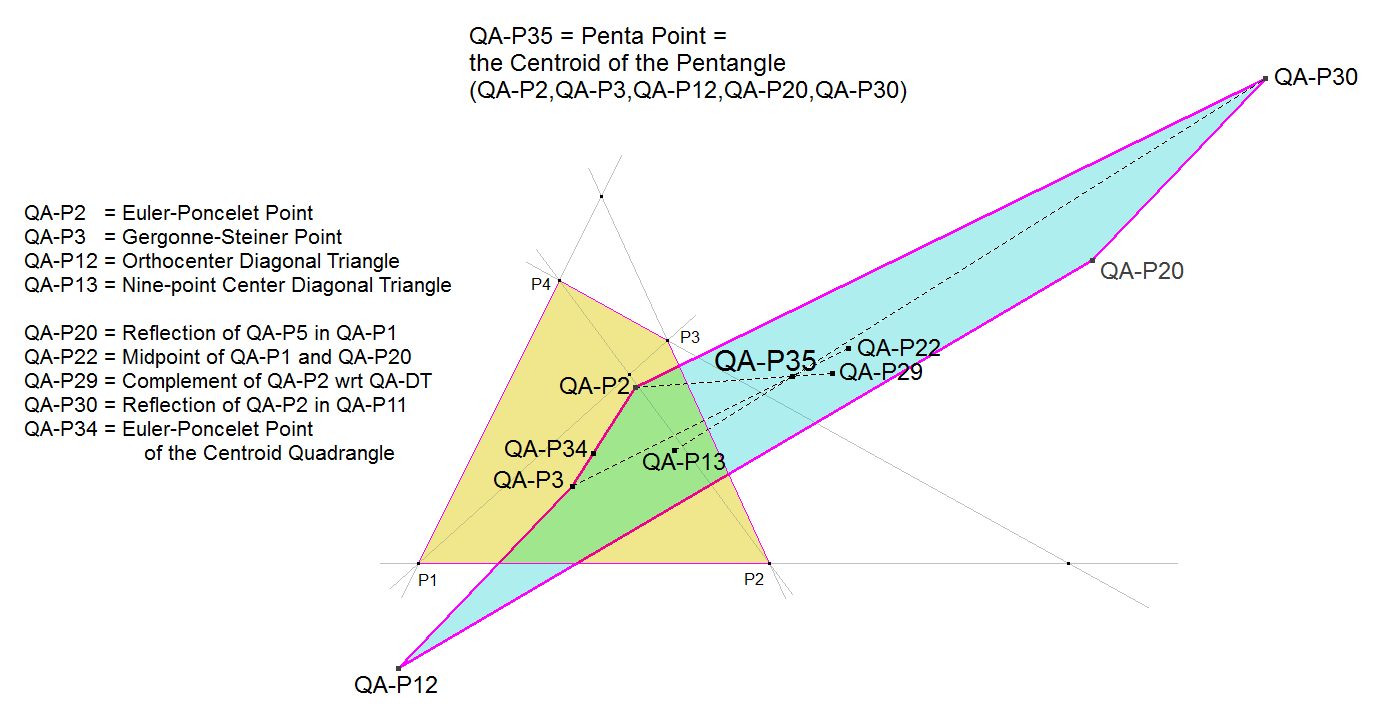
QA-P35: 1st Penta Point
QA-P35 is the Centroid of the Complete Pentangle (system of 5 random points) formed by the points QA-P2, QA-P3, QA-P12, QA-P20, QA-P30. Since there are other Penta Points possible this point is called the 1st Penta Point.
A property from a Pentangle is that its Centroid lies on the lines from each vertice of the Pentangle to the QA-Centroid of the Quadrangle formed by the remainder of its vertices, where the Pentangle Centroid divides these lines in segments with ratio 1 : 4.
Since
we know that QA-P35 is dividing the line segments QA-P13.QA-P30, QA-P22.QA-P3 and QA-P29.QA-P2 in segments with ratio 1 : 4.
Also noteworthy in this specific construction is that:
QA-P35 has another special property.
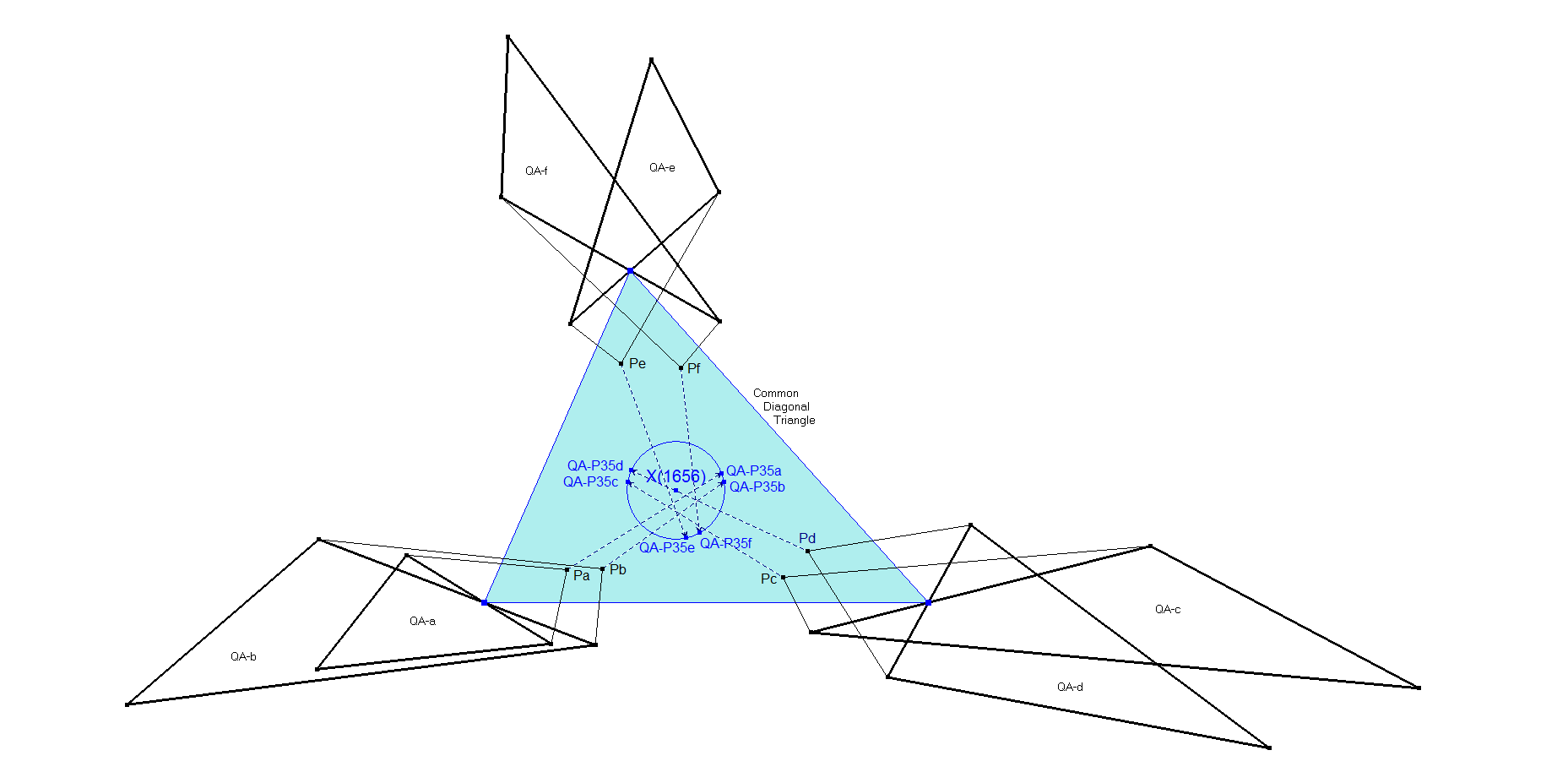
For all Quadrangles with the same Diagonal Triangle QA-P35 lies on a fixed QA-DT-circle. This was observed by Eckart Schmidt. The radius of this circle = 1/5 * radius circumscribed circle QA-DT. See [34], QFG-messages #1666 (item 11), #1674, #1675, #1676.
The center of this circle is X(1656) of the Diagonal Triangle. X(1656) is the intersection point of the Eulerline and the X(17)X(18) Line. See ETC at [12].
1st CT-Coordinate
-4 a4 q (p + q) r (p + r) (2p+q+r) – b2 c2 (q + r) (p3 q + p2 q2 + p3 r – 12 p2 q r – 5 p q2 r + p2 r2 – 5 p q r2 + 2 q2 r2)
-b4 (p + q) r (q + r) (7 p2 + 3 p q + 3 p r – q r) + a2 c2 q (p + r) (p2 q + p q2 + 15 p2 r + 8 p q r + q2 r + 7 p r2 – q r2)
-c4 q (p + r) (q + r) (7 p2 + 3 p q + 3 p r – q r) + a2 b2 (p + q) r (15 p2 q + 7 p q2 + p2 r + 8 p q r – q2 r + p r2 + q r2)
1st DT-Coordinate
-a4 q2 r2 – 2 b4 p2 r2 – 2 c4 p2 q2
+ a2 c2 q2 (p2 – 2 q2 + 2 r2) + a2 b2 r2 (p2 + 2 q2 – 2 r2) + b2 c2 p2 (-p2 + 2 q2 + 2 r2)
Properties
- QA-P35 lies on these QA-lines:
Estimated human page views: 695
