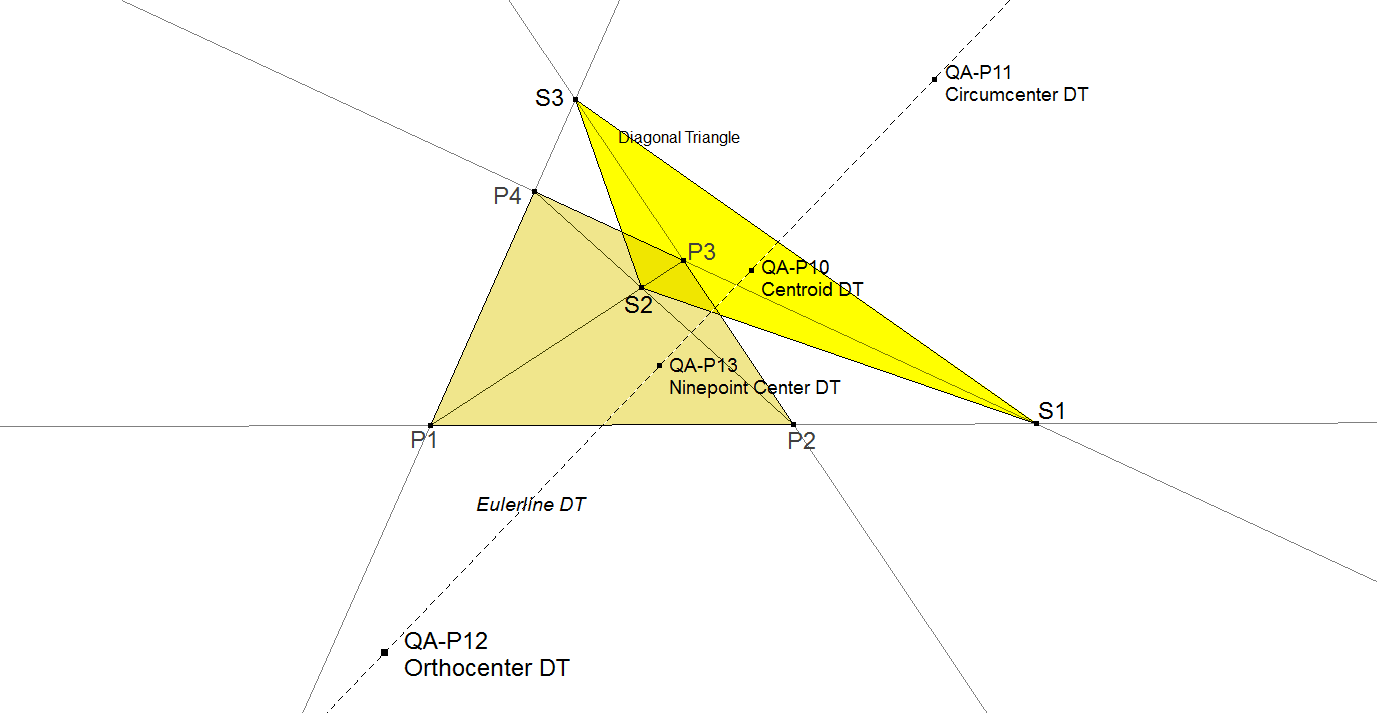
QA-P12: Orthocenter of the QA-Diagonal Triangle
QA-P12 is the Orthocenter of the Diagonal Triangle (QA-Tr1) of a Quadrangle.
1st CT-Coordinate:
(2 SA p2 q r + TA) (a2 q r + SB p q + SC p r) ,
where:
TA = -a2 q2 r2 + b2 p2 r2 + c2 p2 q2
1st DT-Coordinate:
SB SC
Properties:
- QA-P12 lies on these QA-lines:
- QA-P12 is the Involutary Conjugate (see QA-Tf2) of QA-P23.
- QA-P12 is the Antipode of QA-P30 in the QA-DT-P3-P12 Orthogonal Hyperbola (QA-Co4).
- QA-P12 is the Isotomic Center (QA-P5) of the Circumcenter Quadrangle (Eckart Schmidt, August 24, 2012).
- QA-P11 is the QA-Orthopole (QA-Tf3) of QA-P12.
- QA-P12 is the Orthology Center of the QG-P1 Triple Triangle wrt the Triple triangles of QG-P2/QG-P4/QG-P8/QG-P15/QL-P10/QL-P12. See QA-Tr-1.
- QA-P12 is the Orthology Center of the QG-P17 Triple Triangle wrt the Triple triangles of QG-P1/QG-P2/QG-P4/QG-P8/QG-P15/QL-P12. See QA-Tr-1.
- QA-P12 is the Orthology Center of the QL-P10 Triple Triangle wrt the Triple triangles of QG-P2/QG-P4/QG-P8/QG-P15/QL-P12. See QA-Tr-1.
Estimated human page views: 693
