← Previous Next →

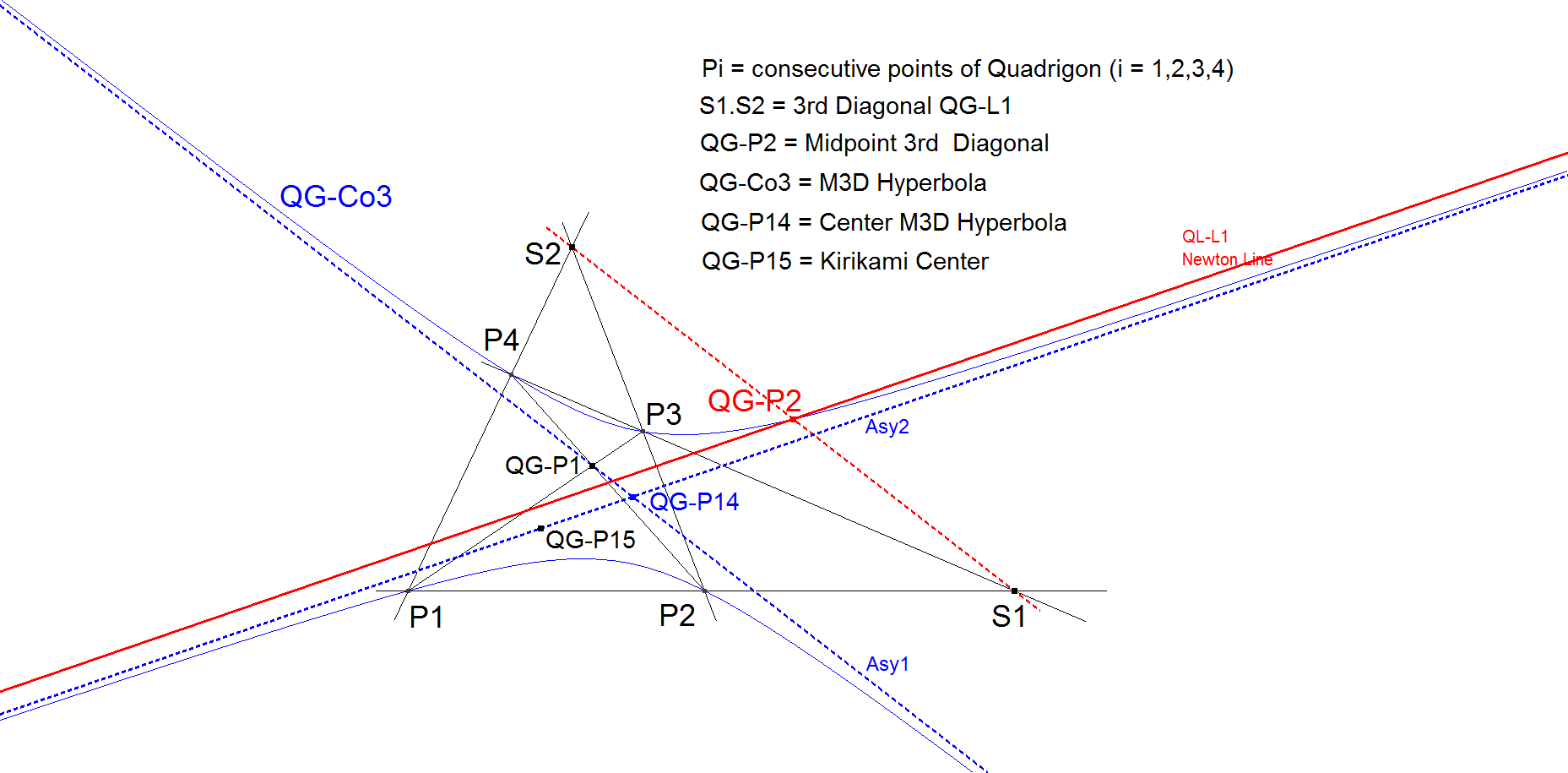
QG-Co3: M3D Hyperbola

QG-Co3 is the conic through the 4 defining points P1, P2, P3, P4 of the Quadrigon and the midpoint of the 3rd Diagonal.

This conic is a hyperbola because there are 2 constructible asymptotes. For a discussion on this conic and related properties see [11] Hyacinthos Message #20183.

Construction asymptotes and center

The 1st asymptote Asy1 is parallel to the 3rd Diagonal (QG-L1) and the 2nd asymptote Asy2 is parallel to the Newton Line (QL-L1). The Diagonal Crosspoint (QG-P1) lies on Asy1. So Asy1 can be constructed by drawing the line through QG-P1 parallel to the 3rd Diagonal.

The Center of the conic (QG-P14) is the Reflection of QG-P1 in intersection point (Asy1 ^ Newton Line). So Asy2 can be constructed by drawing the line through Ce parallel to the Newton Line.

Note 1: The Reflection of QG-P1 in QG-P2 lies on Asy2.

Note 2: QG-P1 is a railway watcher (see paragraph QL-L-1: Railway Watcher) of the Newton Line and Asy2.

Infovisual QG-Co3-infovisual-cvt-01.png
Equation QG-Co3 in 3 QA-Quadrigons in CT-notation

p q (p + q)2 r2 x y – p q2 (p – r) r (p + 2 q + r) x z – p2 q r (q + r)2 y z

p (p – q) q r2 (p + q + 2 r) x y – p q2 r (p + r)2 x z + p2 q r (q + r)2 y z

p q (p + q)2 r2 x y – p q2 r (p + r)2 x z – p2 q (q – r) r (2 p + q + r) y z

Equation QG-Co3 in 3 QL-Quadrigons in CT-notation

l2 n x y + l m n y2 + l2 m x z – 2 l m n x z + m n2 x z + l n2 y z

l2 n x y – 2 l m n x y + m2 n x y + l2 m x z + l m2 y z + l m n z2

l m n x2 + m2 n x y + m n2 x z + l m2 y z – 2 l m n y z + l n2 y z

Equation QG-Co3 in 3 QA-Quadrigons in DT-notation

(p2 – r2) y2 + q2 (z2 – x2)

(r2 – q2) x2 + p2 (y2 – z2)

(q2 – p2) z2 + r2 (x2 – y2)

Equation QG-Co3 in 3 QL-Quadrigons in DT-notation

(x + z) (x l2 + z n2) – y2 m2

(y + z) (y m2 + z n2) – x2 l2 

(x + y) (x l2 + y m2) – z2 n2

Properties
  • The Center of QG-Co3 is QG-P14.
  • QG-P2 lies on QG-Co3.
  • The asymptotes of QG-Co3 are QG-P14.QG-P1 and QG-P14.QG-P15.
  • In a QL-Quadrigon QG-P15 is the 3rd intersection point of the QG-Co3 Hyperbolas of the other two QL-Quadrigons.
  • This conic is the locus of Centers of involution of all lines // Newton Line (QL-L1). See paragraph QA-Tf1: Line Involution Center. This is an example of a combination of QA- and QL-properties in a Quadrigon (which can be seen as the intersection of a Quadrangle and a Quadrilateral).


Estimated human page views: 525

Scroll naar boven