← Previous Next →

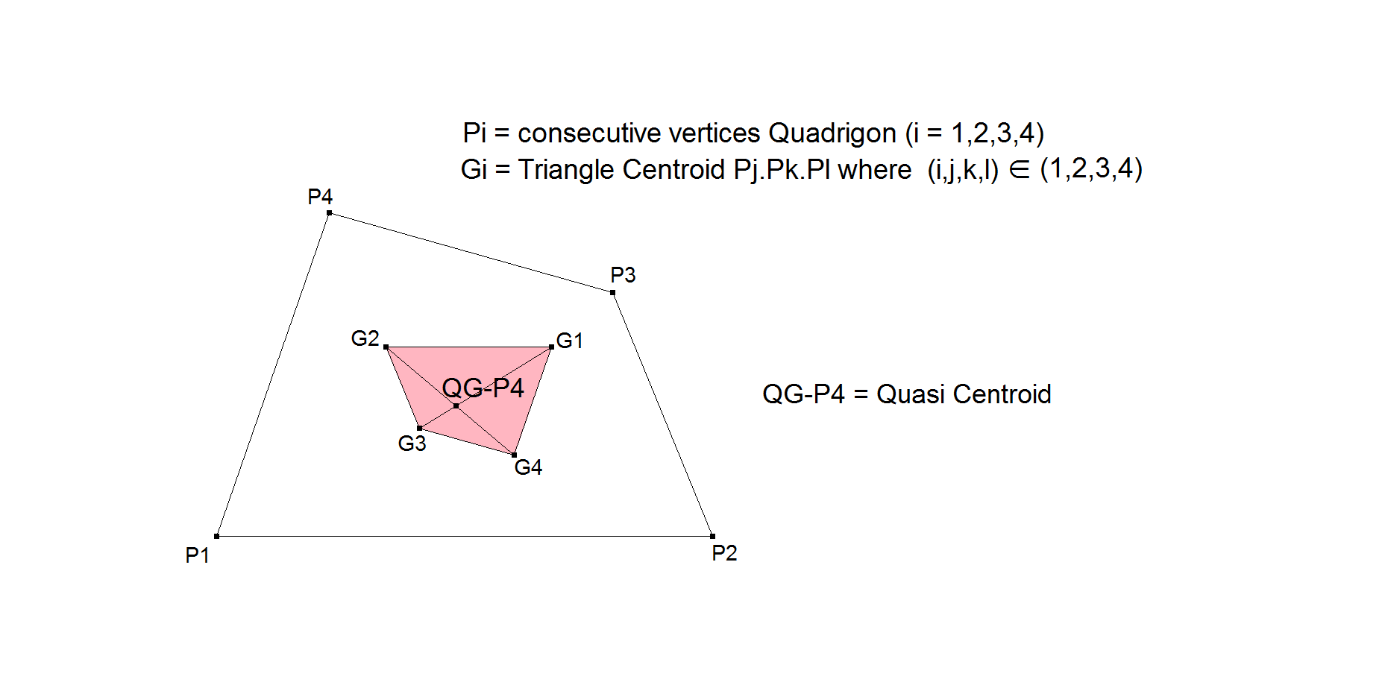
QG-P4: 1st Quasi Centroid

The 1st Quasi Centroid is the Diagonal Crosspoint of the X2-Quadrigon.

The X2-Quadrigon is defined by its vertices being the Triangle Centroids of the component triangles of the Reference Quadrigon.

This point is actually the center of mass of the Quadrigon when it is convex and when its surface is being made of some evenly distributed material.

This point and other 1st Quasi points are described in [5].

Infovisual QG-P4-infovisual-cvt-01.png
CT-Coordinates QG-P4 in 3 QA-Quadrigons

((p + r)2 + q r : (p + r) (p + 2q + r) : (p + r)2 + p q )

((q + r) (2p + q + r) : (q + r)2 + p r : (q + r)2 + p q )

((p + q)2 + q r : (p + q)2 + p r : (p + q) (p + q + 2r) )

CT-Coordinates QG-P4 in 3 QL-Quadrigons

* ((lm+ln+mn)2-lmn(l+4m+4n) : (n-l)(lm2+l2n+m2n-2lm(-l+m+n)) : (m-l)(ln2+l2m+mn2)-2ln(-l+m+n))

* ((n-m)(l2m+m2n+l n-2lm(l-m+n)) : (lm+ln+mn)2-lmn(4l+m+4n) : (l-m)(lm2+mn2+ln2-2mn(l-m+n)))

* ((m-n)(l2m+l2n+mn2-2ln(l+m-n)) : (l-n)(lm2+m2n+ln2-2mn(l+m-n)) : (lm+ln+mn)2-lmn(4l+4m+n))

CT-Area of QG-P4-Triangle in the QA-environment

2 p q r Δ / (9 (p + q) (p + r) (q + r)) (equals 1/9 * area QA-Diagonal Triangle)

CT-Area of QG-P4-Triangle in the QL-environment

4 l2 m2 n2 Δ /(9 (-lm+ln+mn) (lm+ln-mn) (lm-ln+mn)) (equals 1/9 * area QL-Diagonal Triangle)

–

DT-Coordinates QG-P4 in 3 QA-Quadrigons

(-4 p2 (p2-q2-r2) : (p2-r2)2 -2 q2 (-p2+q2-r2)- q4 : -4 r2 (-p2-q2+r2))

((r2-q2)2 -2 p2 (-r2+p2-q2)- p4 : -4 q2 (-r2-p2+q2) : -4 r2 (r2-p2-q2))

(-4 p2 (-q2-r2+p2) : -4 q2 (q2-r2-p2) : (q2-p2)2 -2 r2 (-q2+r2-p2)- r4)

DT-Coordinates QG-P4 in 3 QL-Quadrigons

(2 m2 (m2-n2) : -m2 (l2+m2+n2)+3 l2 n2 : 2 m2 (-l2+m2))

(- l2 (l2+m2+n2)+3 n2 m2 : 2 l2 (-n2+l2) : 2 l2 (l2-m2))

(2 n2 (-m2+n2) : 2 n2 (n2-l2) : -n2 (l2+m2+n2)+3 m2 l2)

DT-Area of QG-P4-Triangle in the QA-environment

S / 18 (equals 1/9 * area QA-Diagonal Triangle)

DT-Area of QG-P4-Triangle in the QL-environment:

S / 18 (equals 1/9 * area QL-Diagonal Triangle)

Properties
  • QG-P4, QG-P5, QG-P6, QG-P7 are collinear on QG-L4, the 1st QG-Quasi Euler Line.
  • QG-P1, QG-P4, QG-P8, QG-P15, QA-P1 are collinear on QG-L3, the QG-Centroids Line.
  • QG-P4 is the Reflection of QG-P1 in QG-P8.
  • QG-P4 is the Reflection of QG-P8 in QA-P1 (QA-Centroid).
  • QG-P4 is the Reflection of QA-P10 (Centroid QA-DT) in QL-P12 (QL-Centroid) (Eckart Schmidt, July, 2012) !
  • QG-P4 is the Centroid of the 1st QG-Quasi Diagonal Triangle: QG-Tr1.
  • QG-P4 is the Centroid of the Triangle formed by QA-P5 and the two vertices of the QA-Diagonal Triangle unequal QG-P1.
  • QA-P25 is the Centroid of the triangle formed by the 3 QA-versions of QG-P4.
  • QL-P14 is the Centroid of the triangle formed by the 3 QL-versions of QG-P4.
  • Divide the sides of a Quadrigon into three equal parts. The figure formed by connecting and extending adjacent points on either side of the Quadrigon form a parallelogram, Wittenbauer’s Parallelogram. See [13]. QG-P4 is the center of this parallelogram.
  • QA-P34 lies on the circle defined by the 3 QA-versions of QG-P4 (note Eckart Schmidt).
  • The triangle formed by the 3 QA-versions of QG-P4 is homothetic and perspective with the QA-Diagonal Triangle. The side lengths are 1/3 of the side lengths of the QA-Diagonal triangle. Their Perspector is QA-P1.
  • The area of the triangle formed by the 3 QA-versions of QG-P4 equals 1/9 * the area of the QA-Diagonal Triangle.
  • The area of the triangle formed by the 3 QL-versions of QG-P4 also equals 1/9 * the area of the QL-Diagonal Triangle. However both triangles are not homothetic neither perspective.


Estimated human page views: 1199

Scroll naar boven