← Previous Next →

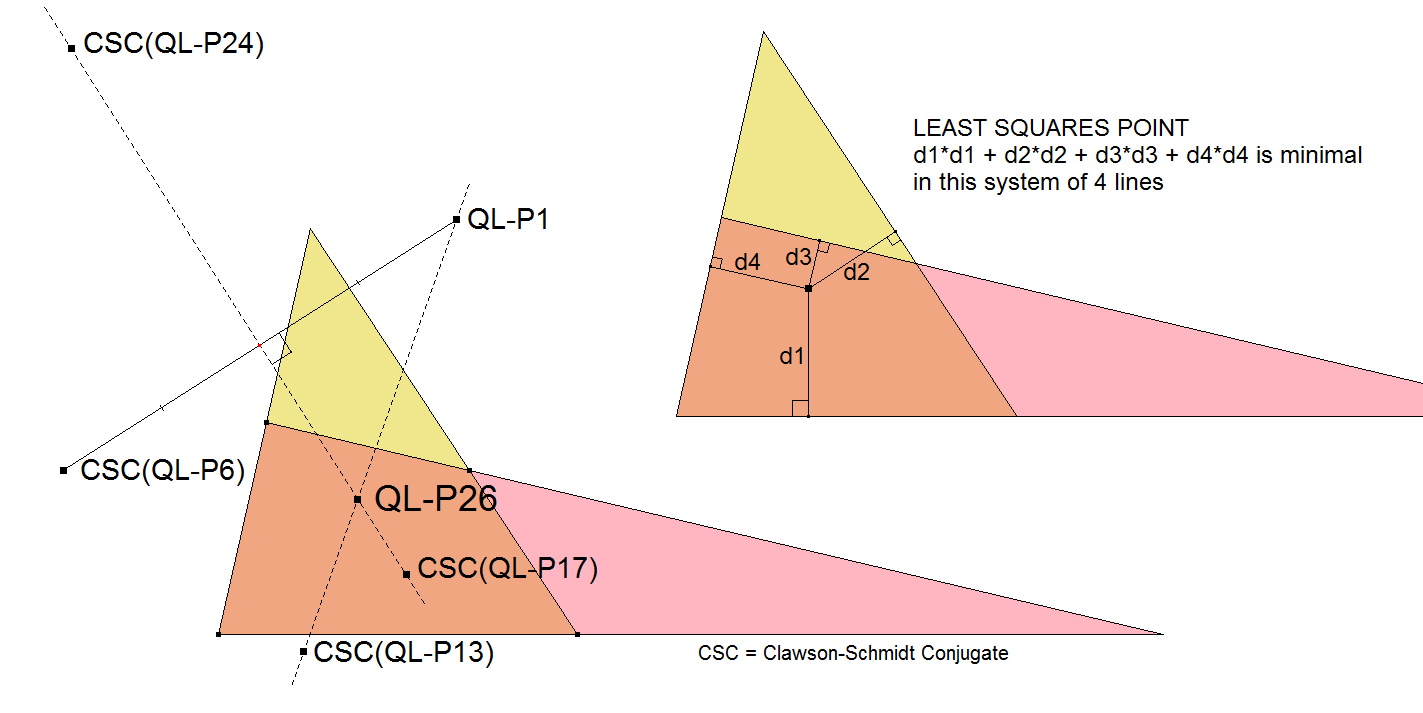
QL-P26: Least Squares Point

QL-P26 is the point in a quadrilateral such that the sum of the squares of the distances to the 4 basic lines is minimal.

Infovisual QL-P26-infovisual-cvt-01.png
Infovisual QL-P26-infovisual-cvt-02.png
Construction 1:
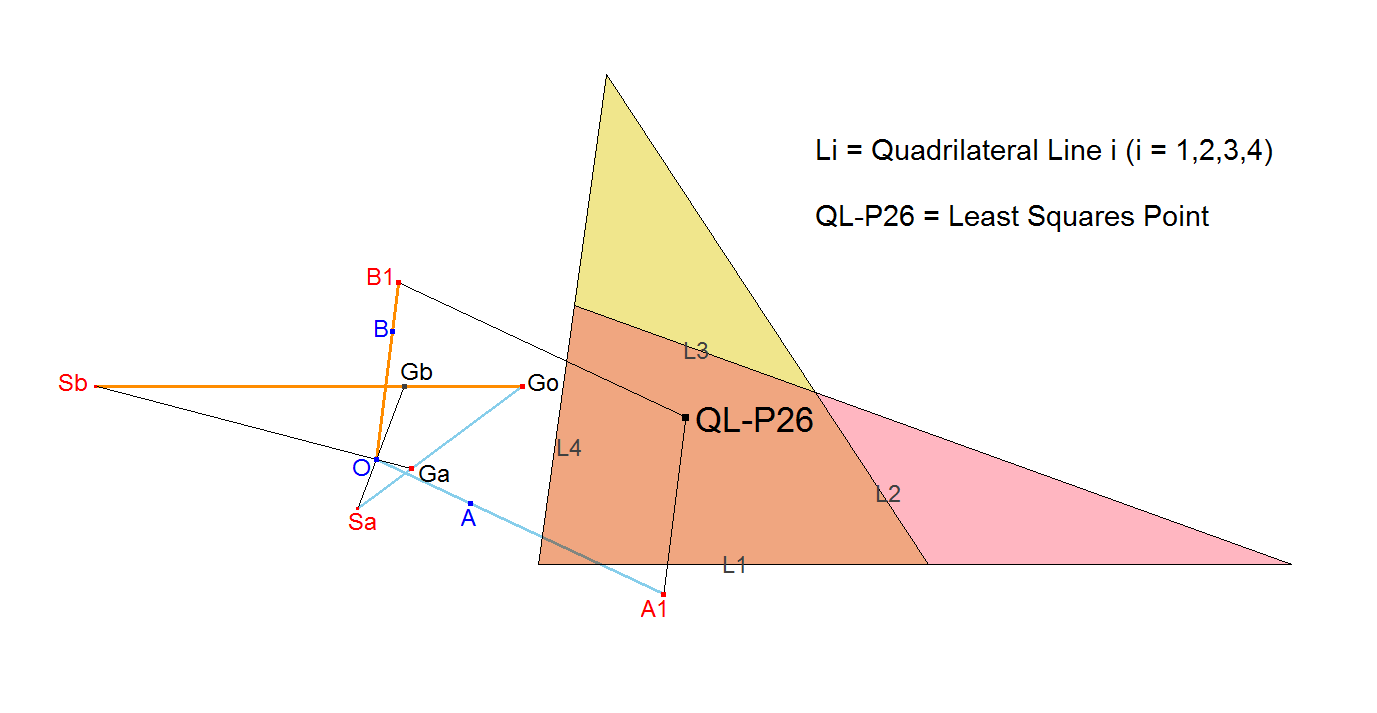
Infovisual QL-P26-infovisual-cvt-03.png

This construction is a modified version of the construction of Coolidge as described in [25].

  • Let O (origin), A and B be random non-collinear points.
  • Go = Quadrangle Centroid of the projection points of O on the 4 basic lines of the Reference Quadrilateral.
  • Ga = Quadrangle Centroid of the projection points of O on the 4 lines through point A parallel to the 4 basic lines of the Reference Quadrilateral.
  • Gb = Quadrangle Centroid of the projection points of O on the 4 lines through point B parallel to the 4 basic lines of the Reference Quadrilateral.
  • Let Sa = Ga.Go ^ O.Gb and Sb = Gb.Go ^ O.Ga.
  • Construct A1 on line O.A such that Sa.Ga : Ga.Go = O.A : A.A1.
  • Construct B1 on line O.B such that Sb.Gb : Gb.Go = O.B : B.B1.
  • Construct P such that O.A1.P.B1 is a parallelogram and where O and P are opposite vertices. P is the Least Squares Point QL-P26.
Construction 2

Here follows an alternative construction of QL-P26 derived from the property found by Eckart Schmidt (October 5, 2012) that in a Quadrigon QL-P26 is the Centroid of its pedal Quadrangle:

  1. Let P1, P2, P3 P4 be the intersection points of L1, L2, L3, L4 in some QL-Quadrigon.
  2. Let G1a and G1b be the Centroids of the pedal Quadrangles of random points Q1a, Q1b on the perpendicular through P1 to P3.P4. Let T1 = Q1a.Q1b ^ G1a.G1b.
  3. Let G2a and G2b be the Centroids of the pedal Quadrangles of random points Q2a, Q2b on the perpendicular through P2 to P3.P4. Let T2 = Q2a.Q2b ^ G2a.G2b.
  4. Let G3a and G3b be the Centroids of the pedal Quadrangles of random points Q3a, Q3b on the perpendicular through P3 to P1.P2. Let T3 = Q3a.Q3b ^ G3a.G3b.
  5. Let G4a and G4b be the Centroids of the pedal Quadrangles of random points Q4a, Q4b on the perpendicular through P4 to P1.P2. Let T4 = Q4a.Q4b ^ G4a.G4b.
  6. Now QL-P26 = T1.T2 ^ T3.T4.
Construction 3

There is another remarkable construction of QL-P26 described by M. Léon Ripert. See [45], pages 110-112 and [43] QFG #457.

  • Let L1.L2.L3 be a reference triangle with 4th Line L4 crossing the 3 Lines of the reference triangle.
  • Q4 = L1 ^ ((L2^L3)-Symmedian of triangle L2.L3.L4)
  • R4 = L2 ^ ((L3^L1)-Symmedian of triangle L3.L1.L4)
  • S4 = L3 ^ ((L1^L2)-Symmedian of triangle L1.L2.L4)
  • Q4, R4, S4 are collinear on a line SL4.
  • For the other 3 Component triangles corresponding lines SL1, SL2, SL3 can be constructed.
  • These 4 Lines concur in QL-P26.

Coordinates:

1st CT-coordinate

a2 (a2 (l – m) (l – n) + b2 (2 m – n) (m – l) + c2 (2 n – m) (n – l))

Least Sum of 4 Square Distances in CT-notation:

(-a4 m2 n2 (l – m) (l – n) + b2 c2 l2 (m – n)2 ((l + m + n) (2 l + m + n) – m n)

– b4 l2 n2 (m – l) (m – n) + c2 a2 m2 (n – l)2 ((l + m + n) (l + 2 m + n) – n l )

– c4 m2 l2 (n – l) (n – m) + a2 b2 n2 (l – m)2 ((l + m + n) (l + m + 2 n) – l m))/

((l + m + n)2 (a2 m n (l – m) (l – n) + b2 n l (m – l) (m – n) + c2 l m (n – l) (n – m)))

–

1st DT-coordinate

m2 n2 (a4 (l2 – m2) (l2 – n2) – b4 (m2 – l2) (m2 – n2) – c4 (n2 – l2) (n2 – m2)

+ 2 a2 b2 (l2 – m2) n2 + 2 a2 c2 m2 (l2 – n2))

Least Sum of 4 Square Distances in DT-notation:

(4 S2 l2 m2 n2 (a2 l2 + b2 m2 + c2 n2))

/ (a4 (l2 – m2) (l2 – n2) (l2 m2 + l2 n2 – m2 n2) + 2 b2 c2 l4 (m2 – n2)2

+ b4 (m2 – n2) (m2 – l2) (l2 m2 – l2 n2 + m2 n2) + 2 c2 a2 m4 (n2 – l2)2

+ c4 (n2 – l2) (n2 – m2) (-l2 m2 + l2 n2 + m2 n2) + 2 a2 b2 n4 (l2 – m2)2)

Properties
  • QL-P26 is collinear with QA-P42 and QG-P12.
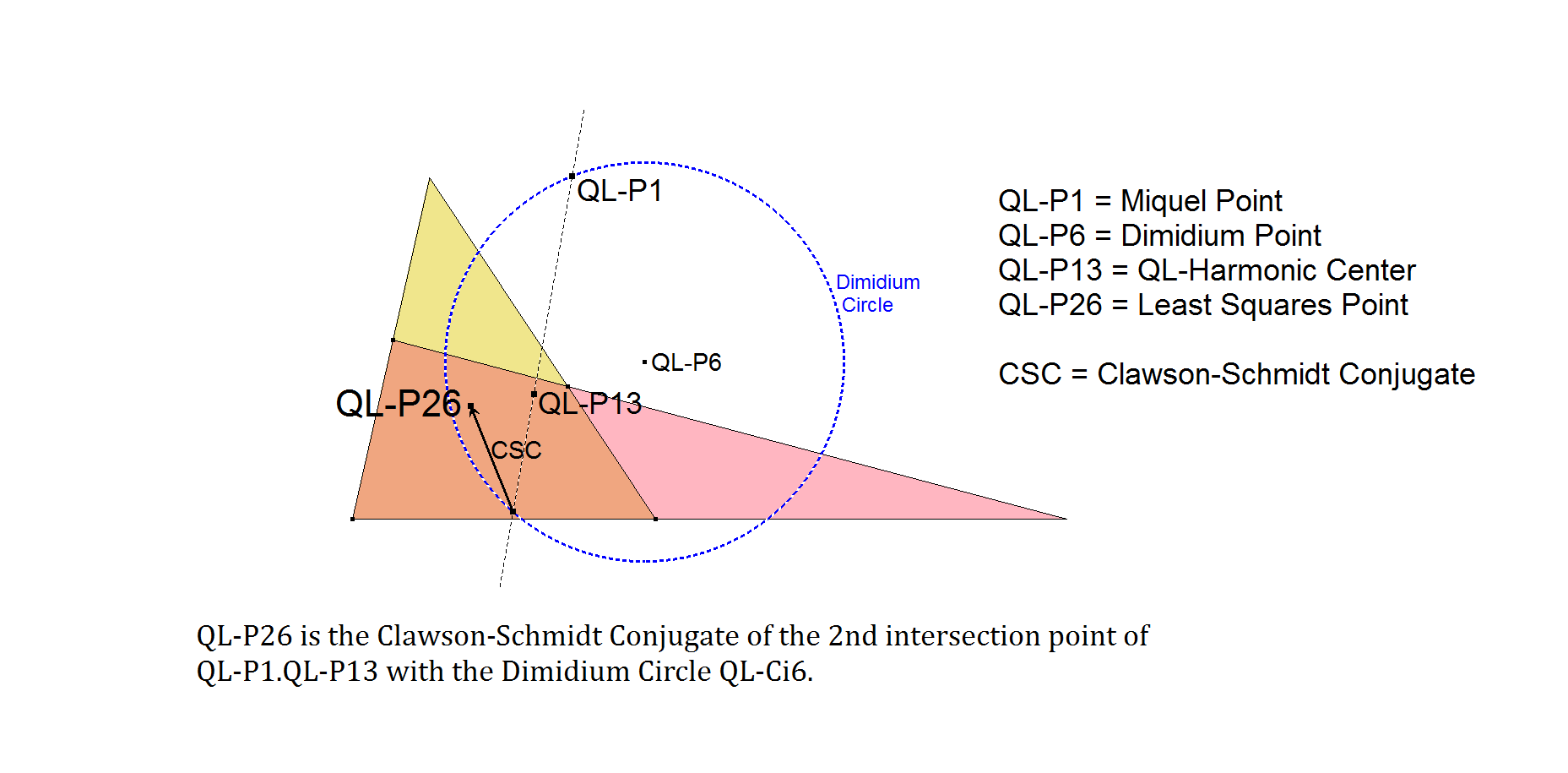
  • QL-P26 is the Clawson-Schmidt Conjugate of the 2nd intersection point of the line QL-P1.QL-P13 with the Dimidium Circle QL-Ci6.
  • QL-P26 lies on the line QL-P1.CSC(QL-P13).
  • (CSC = Clawson-Schmidt Conjugate QL-Tf1)
  • QL-P26 lies on the line QL-L11, which is the line through the 3 QL-versions of QG-P16 as well as the perpendicular bisector of QL-P1.CSC(QL-P6).
  • The three QL-versions of QG-P16 (Schmidt Point) are collinear on former line, which is also the QL-Tf1 image of the Dimidium circle QL-Ci6 (Eckart Schmidt, November 30,2012).
  • In a Quadrigon QL-P26 is the Centroid of its pedal Quadrangle (Eckart Schmidt, October 5, 2012).
  • QL-P26 lies on the orthogonal hyperbola through QL-P1, QL-P19 and the 3 intersection points QL-P1.QA-P4 ^ QL-P19.QA-P6 (constructing per QL-Quadrigon the related QA-P4 point and QA-P6 point) (Eckart Schmidt, October 5, 2012).
  • In a quadrilateral, the three QL-versions of QA-P2 (Euler) and QA-P4 (isogonic) produce inversely similar triangles. The fixed point of this similarity is QL-P26. See [34], QFG-message #1430 of Benedetto Scimemi). With this affine transformation the 3 versions of angle QA-P2i.QL-P26.QA-P4i (i=a,b,c) share the same angle bisectors (additional note of Bendetto).
  • Every Component Triangles has a conic Coi (i=1,2,3,4) through its vertices, centroid and its perspector with the QL-Diagonal Triangle. The Isogonal conjugate of this conic wrt this Component Triangle is a line ILi (i=1,2,3,4). The 4 lines ILi (i=1,2,3,4) are concurrent in QL-P26. See [34], QFG-messages #457 and #1458 of Bernard Keizer.


Estimated human page views: 517

Scroll naar boven