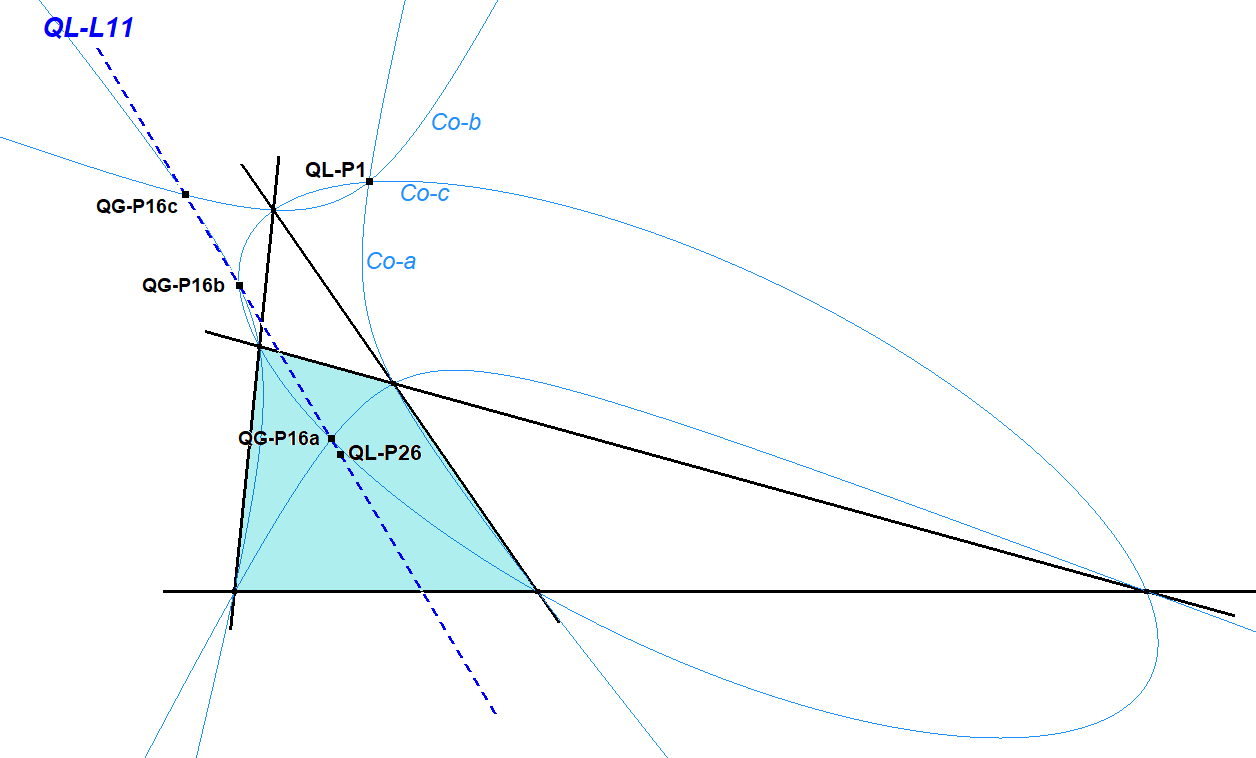
QL-L11 QG-P16 Triple Line

Each Quadrilateral has three Component Quadrigons QL-QGa, QL-QGb and QL-QGc (see QL-3QG1). QL-L11 is the line through the 3 versions of the point QG-P16 in these Component Quadrigons.

Let Co-a be the Conic(QL-P1,vertices QL-QGa), Co-b be the Conic(QL-P1,vertices QL-QGb) and Co-c be the Conic(QL-P1,vertices QL-QGc).

Let QG-P16a be the point QG-P16 in QL-QGa, QG-P16b be the point QG-P16 in QL-QGb, QG-P16c be the point QG-P16 in QL-QGc.

All three conics Co-a, Co-b, Co-c have mutually three points in common and therefore they have per pair a 4^th intersection point.

It appears that QG-P16a is the 4^th intersection point of Co-b and Co-c, QG-P16b is the 4^th intersection point of Co-c and Co-a, QG-P16c is the 4^th intersection point of Co-a and Co-b. The three points QG-P16a, QG-P16b, QG-P16c are collinear on a line with simple coordinates and some special properties.

See [66], QPG-messages #1015-#1021.

1^st CT-coordinate

b²c² l (m-n) (2 a² (l – m) (n – l) + b² (l – m) (m – n) + c² (n – l) (m – n))

Properties

• These points lie on QL-L11:
  • QL-P26 (Least Squares Point)
  • QL-Tf1(QL-P17)
  • QL-Tf1(QL-P24)
  • QL-Tf3(QL-P2.QL-P6)
  • QL-Tf3(QL-P3.QL-P4)
• QL-P6 = QL-Tf3(QL-L11)
• QL-L11 = QL-Tf1(QL-Ci6)
• QL-L11 = QL-Tf6(QL-P1)
• QL-L11 is the perpendicular bisector of QL-P1.QL-Tf1(QL-P6)

Estimated human page views: 168