← Previous Next →

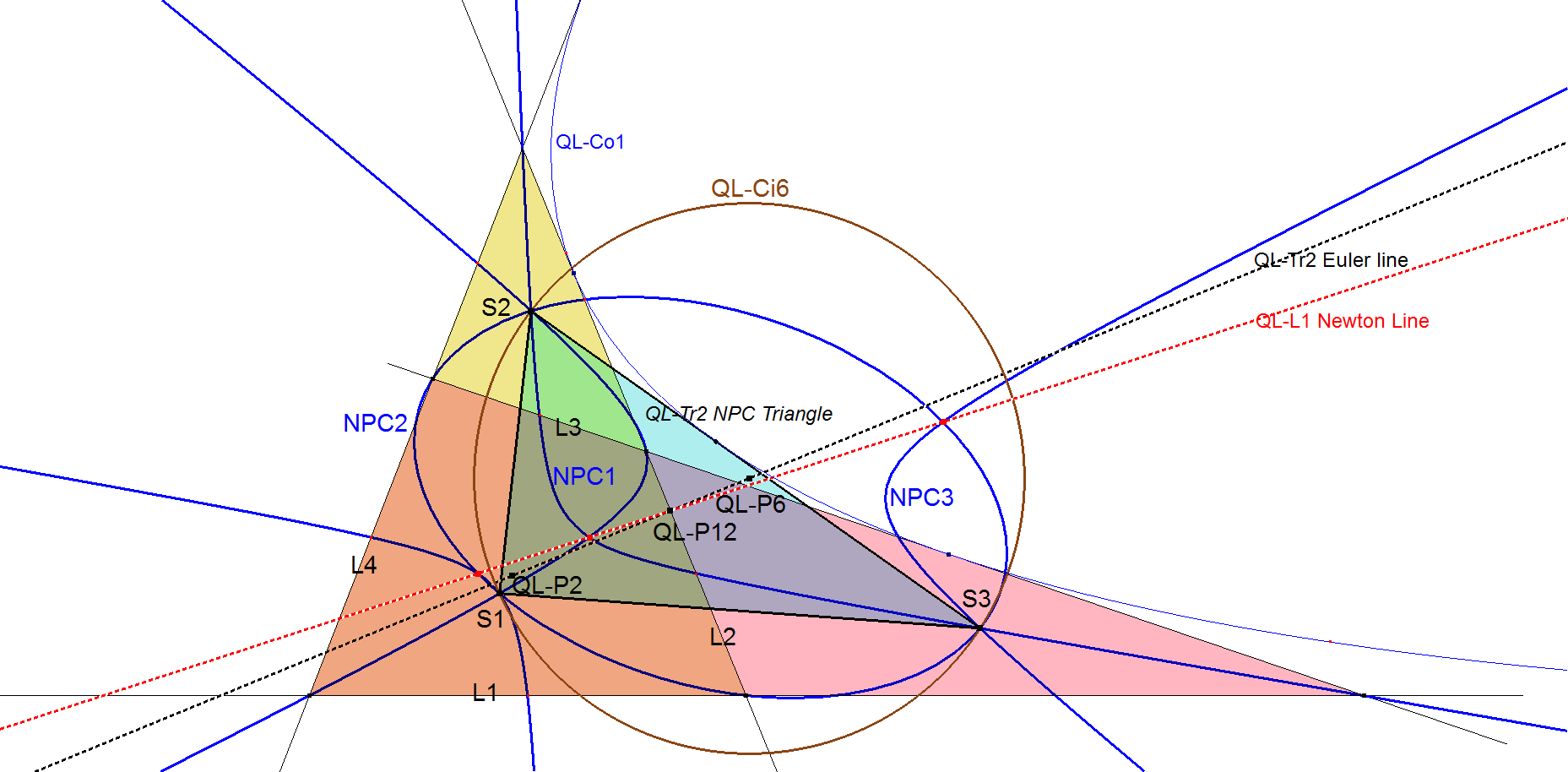
QL-Tr2: NPC-Triangle

The three QA-Ninepoint Conics (QA-Co1) in a Quadrilateral have 3 common points.

Per pair of QA-Ninepoint Conics there is a 4th intersection point that lies on the Newton Line QL-L1. The triangle formed by the 3 common points will be called here the NPC-Triangle (NinePointConic-Triangle). This triangle has several special properties.

More information can be found at [34], QFG#678 in an analyses by Eckart Schmidt, where all properties described below can be found, unless otherwise referenced. Bernard Keizer mentioned these points also at [34], QFG#457 and #1458.

Infovisual QL-Tr2-infovisual-cvt-01.png
CT-coordinates of the 3 vertices

(A1 + B1 + C1 : A2 + B2 + C2 : A3)

(A1 – ½ (1 – i √3) B1 – ½ (1 + i √3]) C1 : A2 – ½ (1 + i √3) B2 – ½ (1 – i √3]) C2 : A3)

(A1 – ½ (1 + i √3) B1 – ½ (1 – i √3]) C1 : A2 – ½ (1 – i √3) B2 – ½ (1 + i √3]) C2 : A3)

where:

A1 -> 3 m (l – n) (2 l2 – 4 l m – l n + 3 m n) U1

B1 -> -3 m (l – n) U12

C1 -> 3 m (l – n) U4

A2 -> 3 l (l – n) (4 l m – 2 m2 – 3 l n + m n) U1

B2 -> U13 – (2 l2 – l m – 4 l n + 3 m n) U4

C2 -> (U42 + (2 l2 – l m – 4 l n + 3 m n) U13)/U1

A3 -> 9 l m (l – m)(l – n) U1

where:

U1 = (-8 l6 + 21 l5 m – 15 l4 m2 + 10 l3 m3 + 21 l5 n – 75 l4 m n + 75 l3 m2 n – 45 l2 m3 n – 15 l4 n2 + 75 l3 m n2 – 90 l2 m2 n2 + 54 l m3 n2 + 10 l3 n3 – 45 l2 m n3 + 54 l m2 n3 – 27 m3 n3 + 3 √(3(-l2 (l – m)2 (l – n)2 (9 l4 m2 – 9 l3 m3 + 9 l2 m4 – 14 l4 m n + 3 l3 m2 n + 3 l2 m3 n – 14 l m4 n + 9 l4 n2 + 3 l3 m n2 – 3 l2 m2 n2 + 3 l m3 n2 + 9 m4 n2 – 9 l3 n3 + 3 l2 m n3 + 3 l m2 n3 – 9 m3 n3 + 9 l2 n4 – 14 l m n4 + 9 m2 n4))))1/3

U4 = -4 l4 + 7 l3 m – 7 l2 m2 + 7 l3 n – 11 l2 m n + 12 l m2 n – 7 l2 n2 + 12 l m n2 – 9 m2 n2

Properties
  • QL-P12 is the centroid of QL-Tr2.
  • QL-P2 is the orthocenter of QL-Tr2.
  • QL-P6 is the circumcenter of QL-Tr2.
  • Consequently is QL-P2.QL-P6 the Eulerline of QL-Tr2.
  • The vertices of QL-Tr2 lie on the Dimidium Circle QL-Ci6.
  • The sides of QL-Tr2 are tangents to the inscribed Quadrilateral Parabola QL-Co1. For an analyses of the triangle formed by the points of tangency see [34], QFG-message #1460.
  • The triangles QL-Tr1 and QL-Tr2 have a common circumconic containing QL-P8, QL-P13, QL-P24.
  • The Isogonal Conjugate of QL-P1 wrt QL-Tr2 is the infinity point of QL-L1.
  • The Isogonal Conjugate of QL-P17 wrt QL-Tr2 is the infinity point of QL-L9.
  • Every QL-Component Triangle has a conic Coi (i=1,2,3,4) through its vertices, centroid and its perspector with the QL-Diagonal Triangle. These 4 conics Coi (i=1,2,3,4) also have 3 common points being the vertices of QL-Tr2 (see [34], Bernard Keizer, QFG#457 and #1458 also for more properties).


Estimated human page views: 571

Scroll naar boven