5P-s-P5

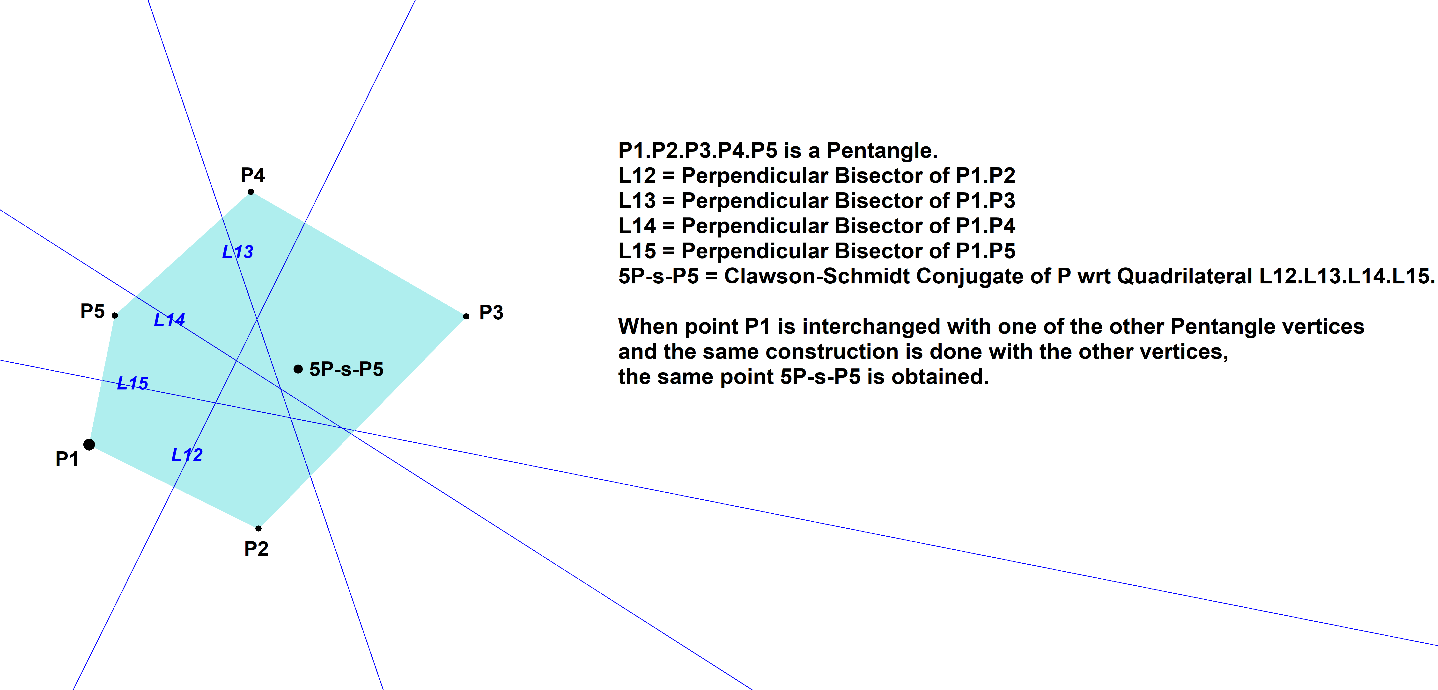
Consider a 5-Point (Pentangle) with vertices Pi (i=1,2,3,4,5).

Choose one of its vertices Pi.

Construct the perpendicular bisectors Lij of (Pi,Pj), where j unequal i.

In this way Pi defines a 4-Line (Quadrilateral) formed by these perpendicular bisectors.

It appears that the Clawson-Schmidt Conjugate (QL-Tf1) wrt to this Quadrilateral of Pi is independent of the chosen Pi. This fixed point is 5P-s-P5.

This point was found by Eckart Schmidt. See [34], QFG #3549.

The coordinates are too complicated to mention here.

In a Triangle 5P-s-P5 of Pentangle ABCBr1Br2 (where Br1, Br2 are the 2 Brocard Points of Triangle ABC) is ETC Center X(98). See [12].
In a Reference Quadrilateral we have 3 Component Quadrigons (see QL-3QG1). For each Component Quadrigon we can construct the circular cubic QA-Cu1.These three cubics have 5 common points, which form a Pentangle extensively discussed in the Quadri-Figures Group, see [34], keywords “3 QL-versions of QA-Cu7” and “5P-Geometry”.The point 5P-s-P5 of this Pentangle coincides with a point U, being the intersection point of the 3 QL-versions of QA-P41.QG-P18 of the Reference Quadrilateral.

Estimated human page views: 254