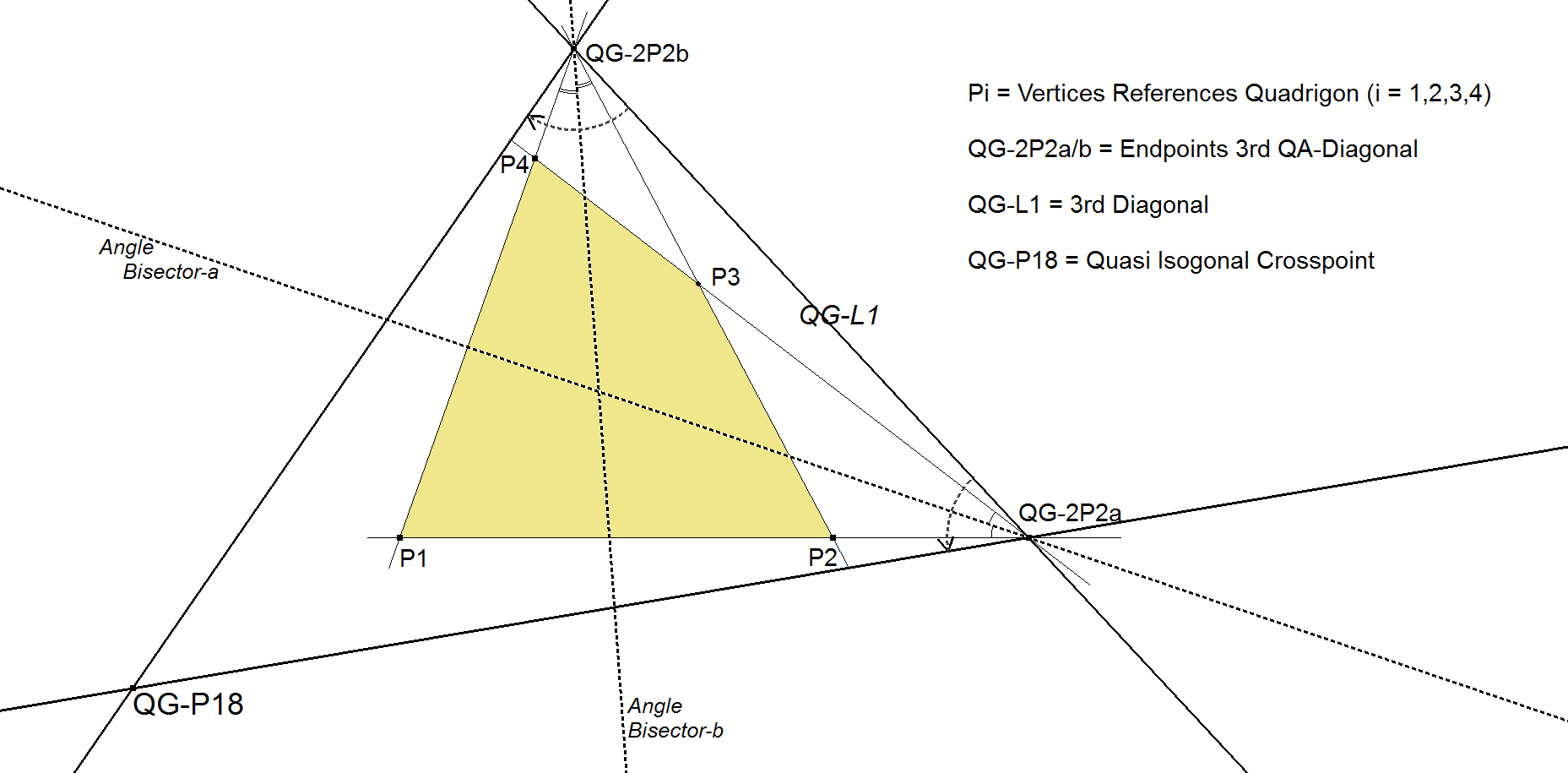
QG-P18: Quasi Isogonal Crosspoint

QG-P18 is the intersection of the reflections of the 3^rd Diagonal QG-L1 in the angle bisectors of the opposite sides of the quadrigon.

This point and its properties are found by Eckart Schmidt (October 5, 2012).

CT-Coordinates in 1^st QA-Quadrigon

(-a² q r ((p + q) (b² p + a² q) r² – c² p q (p q + r²)) :

-p r (b⁴ p (p + q) r (q + r) – (a² – c²) q² (a² (p + q) r – c² p (q + r)) + b² q (-a² (p + q) (p – q – r) r + c² p (p + q – r) (q + r))) :

-c² p q (c² p² q (q + r) + r (b² p² (q + r) – a² q (p² + q r))))

DT-Coordinates in 1^st QA-Quadrigon

((a² – b² – c²) (b² p² + a² q²) :

-(a² – b² – c²) (a² + b² – c²) q² :

-(a² + b² – c²) (c² q² + b² r²))

CT-Coordinates in 1^st QL-Quadrigon

(a² l (a² (l – m) (l – n) + c² (l – n) (m – n) – b² (l m – l n + m n)) :

b² m (a² l² – c² n²) :

c² n (-a² (l – m) (l – n) + c² (l – n) (-m + n) + b² (l m – l n + m n)))

DT-Coordinates in 1^st QL-Quadrigon

(a⁴ (l² – n²) + b² (b² – c²) (m² – n²) + a² (c² (-l² + n²) + b² (l² + m² + 2 n²)) :

a⁴ (-l² + n²) + b⁴ (-l² + n²) + c⁴ (-l² + n²) + 2 b² c² (l² + n²) – 2 a² (c² (-l² + n²) + b² (l² + n²)) :

b⁴ (l² – m²) + c⁴ (l² – n²) – b² c² (2 l² + m² + n²) + a² (b² (-l² + m²) + c² (-l² + n²)))

Properties

• QG-P18 lies on the line through QG-2P5a and QG-2P5b, the intersection points of the QL-DT-Thales Circle (QG-Ci2) with the QG-Diagonals.
• Let S_i = QG-P1, X_i = QG-P18 and Y_i = QG-P19 resp. in QA-Quadrigon-i (i=1,2,3). Now S_i.X_j ^ S_j.X_i = Y_k, S_i.Y_j ^ S_j.Y_i = X_k, X_i.Y_j ^ X_j.Y_i = S_k.
• The Triangles formed by the QA-versions of QG-P1, QG-P18 and QG-P19 are pairwise perspective triangles. Their centers of perspectivity are collinear.
• The Quasi Isogonal Conjugate (QG-Tf2) wrt the Reference Quadrigon is equivalent to the Isogonal Conjugate wrt the Triangle QG-2P2a.QG-2P2b.QG-P18.
• The QG-Tf2 image (Quasi Isogonal Conjugate) of a free line is a conic through QG-P18.
• The QG-Tf2 image (Quasi Isogonal Conjugate) of any point on QG-L1 is QG-P18.
• The QA-Tf2 image (Involutary Conjugate) of QG-P18 is QG-P19.
• QG-P18 is the QL-Tf1 image (Clawson-Schmidt Conjugate) of QG-P17.
• QG-P18 lies concyclic with QG-2P2a, QG-2P2b and QL-P1 (as 4^th intersection of the circle and QL-Cu1).
• QA-P41 lies on the circle defined by the 3 QA-versions of QG-P18.
• The 3 QA-versions of QG-P18 lie on QA-Cu7.
• The 3 QL-versions of QG-P18 are collinear points on QL-Cu1.
• QG-P18 is the second focus of an inscribed conic with its first focus in QG-P17.
• Perpendiculars from QG-P18 to the sidelines of the quadrigon have pedal points on a circle, which is centered in the midpoint of QG-P17 and QG-P18 (this midpoint is a point on the Newton Line QL-L1).
• QG-P18 lies on the Polar (see [13], Polar) of QG-P19 wrt any circumscribed conic of the Reference Quadrigon.
• The Triple Triangle of QG-P18 is perspective with all QA-Component Triangles (see QA-Tr-1 for Desmic Triple Triangles).
• QG-P18 is the common tangential of QG-2P2a,b wrt QL-Cu1. See [66], QPG-message 485.

Estimated human page views: 456