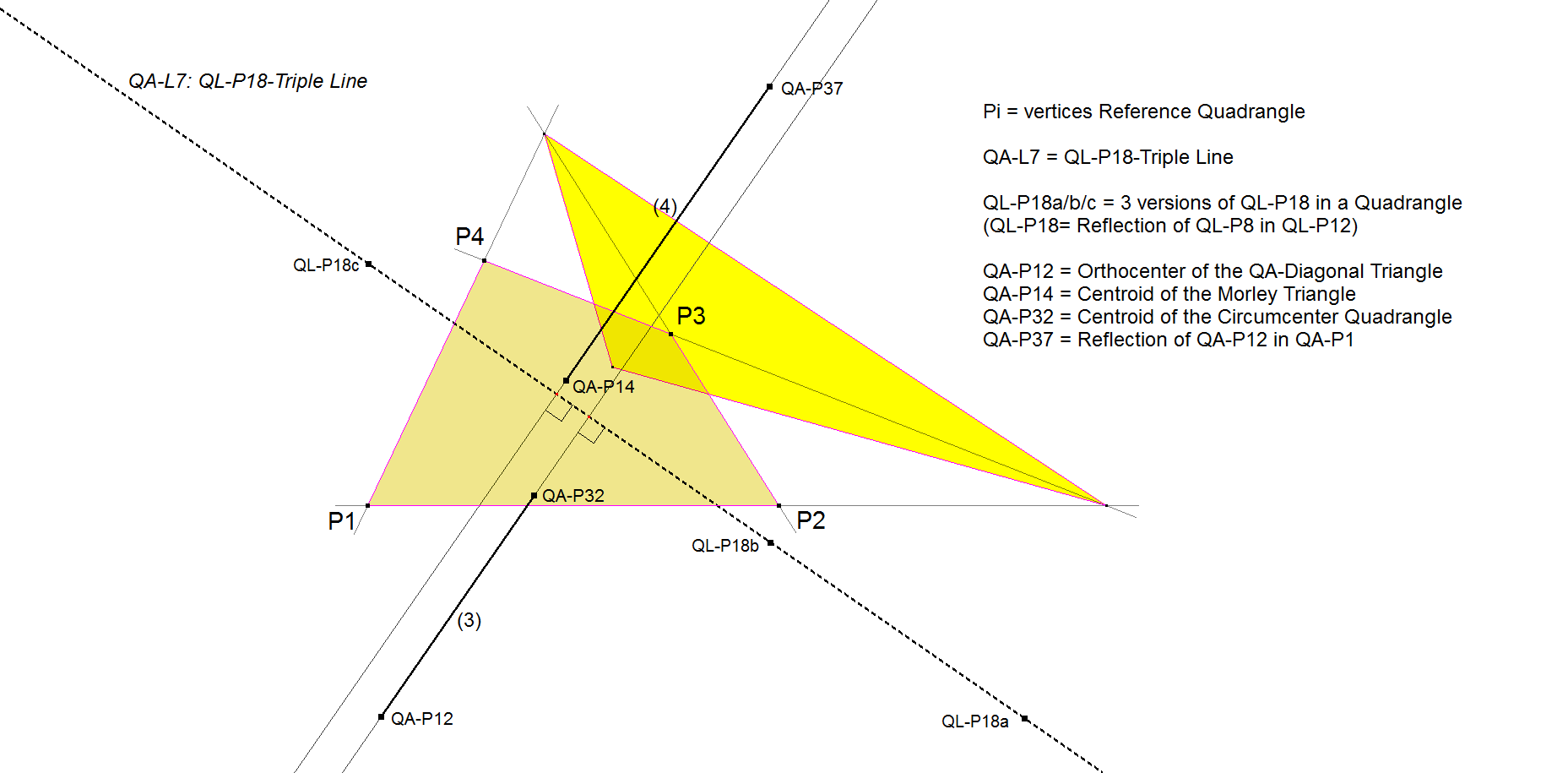
QA-L7: QL-P18-Triple Line

The 3 QA-versions of QL-P18 are collinear and determine the line QA-L7.

This line was found by Eckart Schmidt (November 29, 2012).

Further explanation about a Px-Triple Line can be found at QA-Tr-1.

1st CT-coefficient QA-L7:

-2 q² r² (q + r)² + p⁴ (q² + r²) + p q r (q + r) (q² – 3 q r + r²)

+ p³ (q + r) (2 q² + q r + 2 r²) + p² (q⁴ + 4 q³ r + 4 q² r² + 4 q r³ + r⁴)

1st CT-coordinate Infinity point QA-L7:

p (q² – r²) (3 p (p + q + r) – q r)

1st DT-coefficient QA-L7:

p⁴ (q² + r²) + (q² – r²)(-2p² + q² + r²).

1st DT-coordinate Infinity point QA-L7:

q² – r²

Properties

• QA-L7 is perpendicular to QA-P12.QA-P32 and QA-P14.QA-P37.
• Special about these lines is that the ratio of the lengths of the line segments QA-P12.QA-P32 : QA-P14.QA-P37 = 3 : 4.
• QA-L7 is parallel to one of the asymptotes of the QA-DT circumscribed hyperbola which is the Involutary Conjugate of the line through QA-P22 and its Involutary Conjugate.
• QA-L7 is parallel to the Trilinear Polar of the QA-DT-Isotomic Conjugate of QA-P16 (Eckart Schmidt, November 29, 2012).
• QA-L7 is the QA-Tf2 image  of a QA-DT circumscribed conic with its center in a point, that divides QA-P10.QA-P17 in the ratio -1/3 (Eckart Schmidt, November 29, 2012).

Estimated human page views: 527