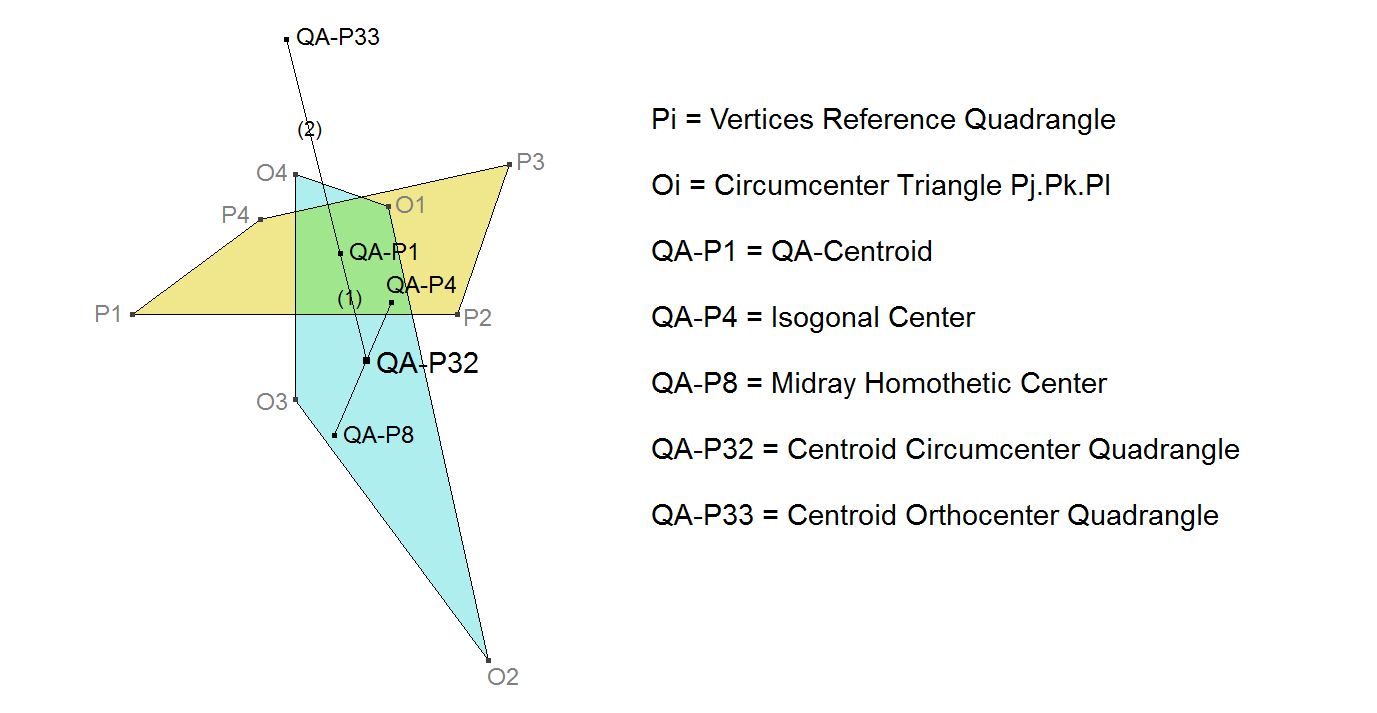
QA-P32: Centroid of the Circumcenter Quadrangle

QA-P32 is the QA-Centroid of the quadrangle formed by the Circumcenters of the Component Triangles of the Reference Quadrangle.

1st CT-Coordinate

-a⁴ q² r² + S_B c² p² q² + S_C b² p² r² + 2 S² p² q r + 3 a² S_A p q r (p + q + r)

1st DT-Coordinate

a⁴ q² r² – S² p⁴ + (c² S_C – S_B²) p² q² + (b² S_B – S_C²) p² r²

Properties

• QA-P32 lies on these QA-lines:
  • QA-P1.QA-P33        (-2 : 3)
  • QA-P4.QA-P8          ( 1 : 1 => QA-P32 = Midpoint QA-P4.QA-P8)
• QA-P1.QA-P32.QA-P33 // QA-P2.QA-P4.QA-P6 = QA-L2.
• QL-P6 is the Centroid of the QL-Triangle formed by the 3 QL-versions of QA-P32 (note Eckart Schmidt).
• The QA-Orthopole(QA-Tf3) of QA-P32 is intersection point QA-P1.QA-P32 ^ QA-P2.QA-P7.
• QA-P32 is the Orthology Center of the QG-P9 Triple Triangle wrt the Triple triangles of QG-P1/QG-P2/ QG-P4/QG-P8/QG-P15/QL-P12. See QA-Tr-1.
• QA-P32 is the Orthology Center of the QG-P5 Triple Triangle wrt the Triple triangles of QG-P12/QG-P14. See QA-Tr-1.
• Let L12, L34, L13, L24, L14, L23 are the perpendicular bisectors of segments P1P2, P3P4, P1P3, P2P4, P1P4, P2P3 respectively. Then Newton lines of the Quadrilaterals (L12,L34, L13,L24) , (L12,L34, L14,L23) and (L13,L24, L14,L23) are concurrent in QA-P32. See [34], Tran Quang Hung, QFG#3735, #3738.

Estimated human page views: 541