QA-P29: Complement of QA-P2 wrt the Diagonal Triangle

QA-P29 is the complement of QA-P2 (Euler-Poncelet Point) wrt the Diagonal Triangle.

1st CT-Coordinate

-2 a⁴ p q r (p + q) (p + r) (q + r) (2 p + q + r)

– b⁴ p r (p + q) (q + r)² (3 p² + p q + p r – q r)

– c⁴ p q (p + r) (q + r)² (3 p² + p q + p r – q r)

– b² c² p (q + r)² (p³ q + p² q² + p³ r – 4 p² q r – p q² r + p² r² – p q r² + 2 q² r²)

+ c² a² p q (p + r) (q + r) (p² q + p q² + 7 p² r + 4 p q r + q² r + 3 p r² – q r²)

+ a² b² p r (p + q) (q + r) (7 p² q + 3 p q² + p² r + 4 p q r – q² r + p r² + q r²)

1st DT-Coordinate

(c² q² – b² r²) ((c² – b²) p² + a² (q² – r²))

Properties

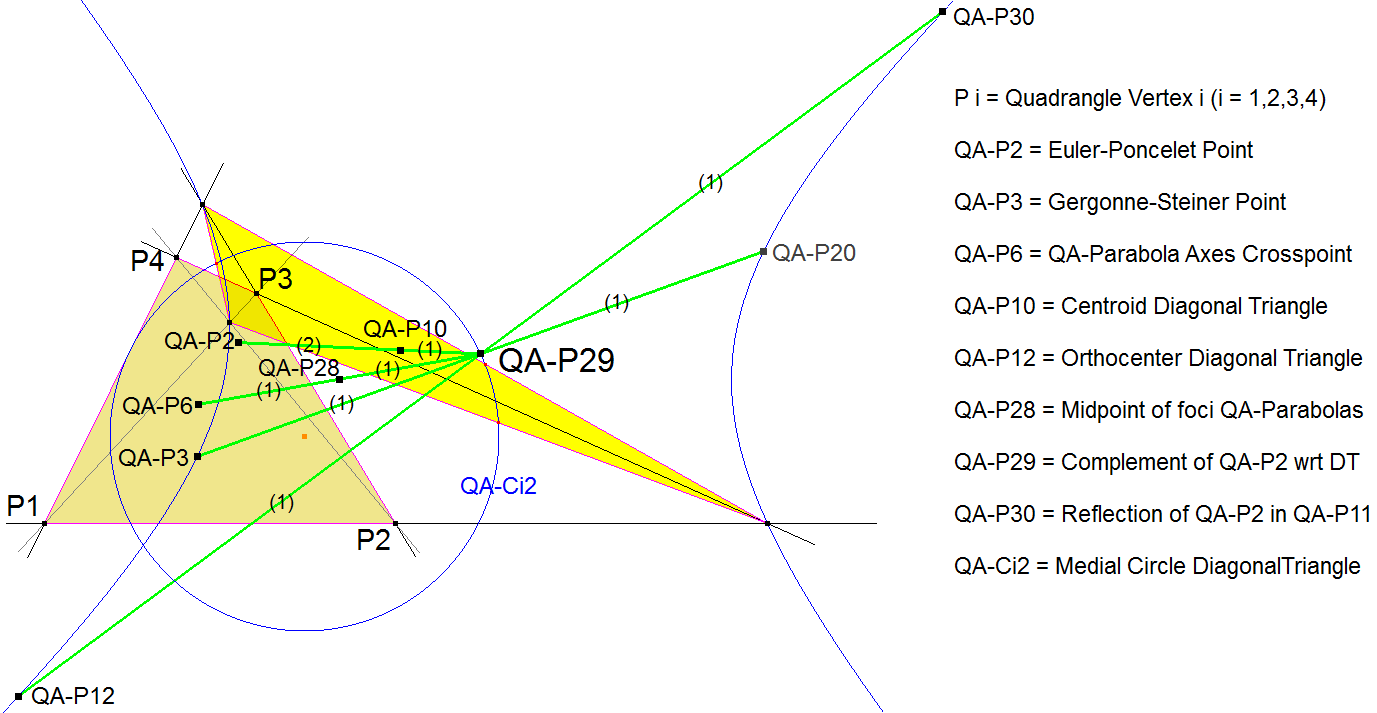
• QA-P29 lies on these QA-lines:
  • QA-P2.QA-P10         (3 : -1 => QA-P29 = Complement QA-P2 wrt QA-DT)
  • QA-P3.QA-P20         (1 : 1 => QA-P29 = Midpoint QA-P3.QA-P20)
  • QA-P5.QA-P34         (3 : -1)
  • QA-P6.QA-P28         (2 : -1 => QA-P29 = Reflection of QA-P6 in QA-P28)
  • QA-P12.QA-P30       ( 1 : 1 => QA-P29 = Midpoint)
  • QA-P13.QA-P36       (-1 : 2 => QA-P29 = Reflection of QA-P36 in QA-P13)
• QA-P29 is the center of the QA-DT-circumscribed orthogonal hyperbola (QA-Co4) additional passing through QA-P3, QA-P12, QA-P20, QA-P30.
• QA-P29 lies on the Medial Circle of the QA-Diagonal Triangle (QA-Ci2).
• QA-P29 lies on the Simson Line of QA-P30 occurring on the circumcircle of the QA-Diagonal Triangle (QA-Ci1).
• QA-P29 = QA-P1 (QA-Centroid) of the Quadrangle QA-P3.QA-P12.QA-P20.QA-P30.
• QA-P29 = QA-P2 (Euler-Poncelet Point) of the quadrangle formed by the vertices of the QA-Diagonal Triangle and QA-P3 of the Reference Quadrangle.
• QA-P29 = QA-P1 (QA-Centroid) of the Quadrangle formed by the DT-vertices + Reflection of QA-P2 in QA-P29.
• If we consider for the QL-inscribed conics the contact QA, their QA-P29 will lie on QL-Ci2. See [66], Eckart Schmidt, QPG-message #1155.

Estimated human page views: 527