QA-P42: QA-Orthopole Center

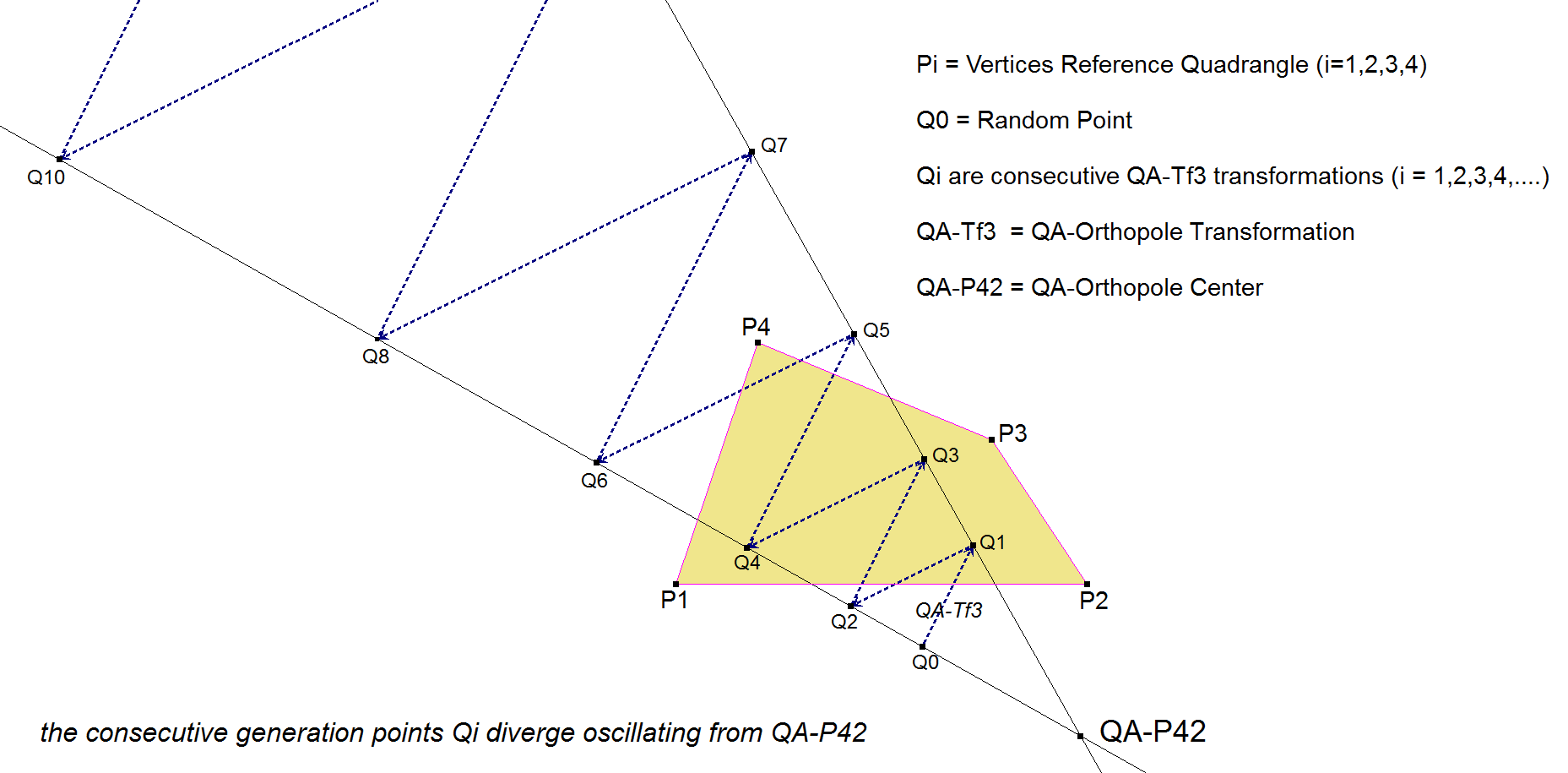
QA-Tf3 is the QA-Orthopole Transformation that transforms a random point Q₀ into another point Q₁. This point Q₁ can again be transformed by QA-Tf3 into another point Q₂, etc..

The lines Q_i.Q_i+2 and Q_i+1.Q_i+3 intersect in a fixed point independent of starting point Q₁.

Stated in another way: the consecutive generation points Qi diverge oscillating from a fixed point. This point will be called QA-P42.

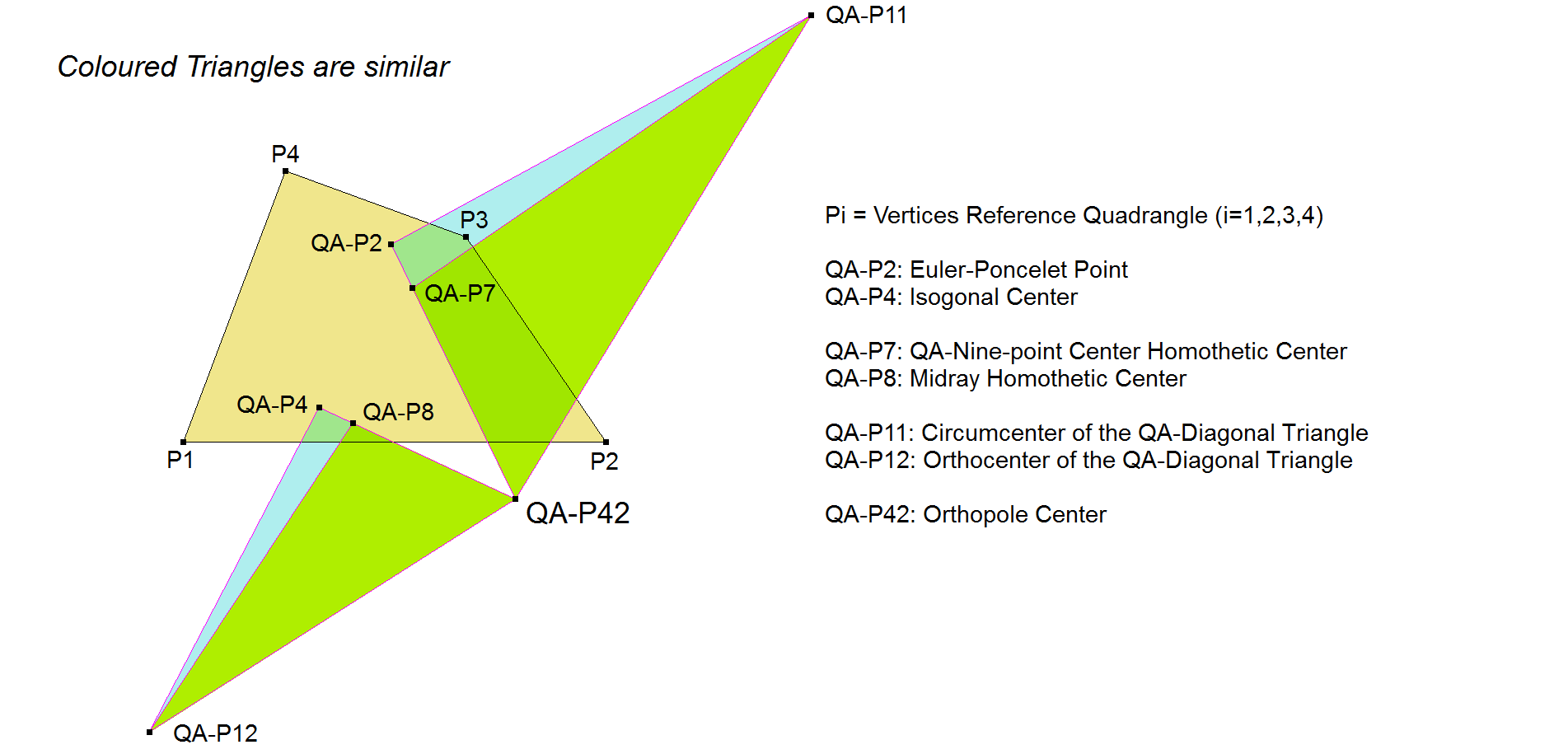
Another interesting and related property is the similarity of Triangles of QA-points and their QA-Tf3-image:

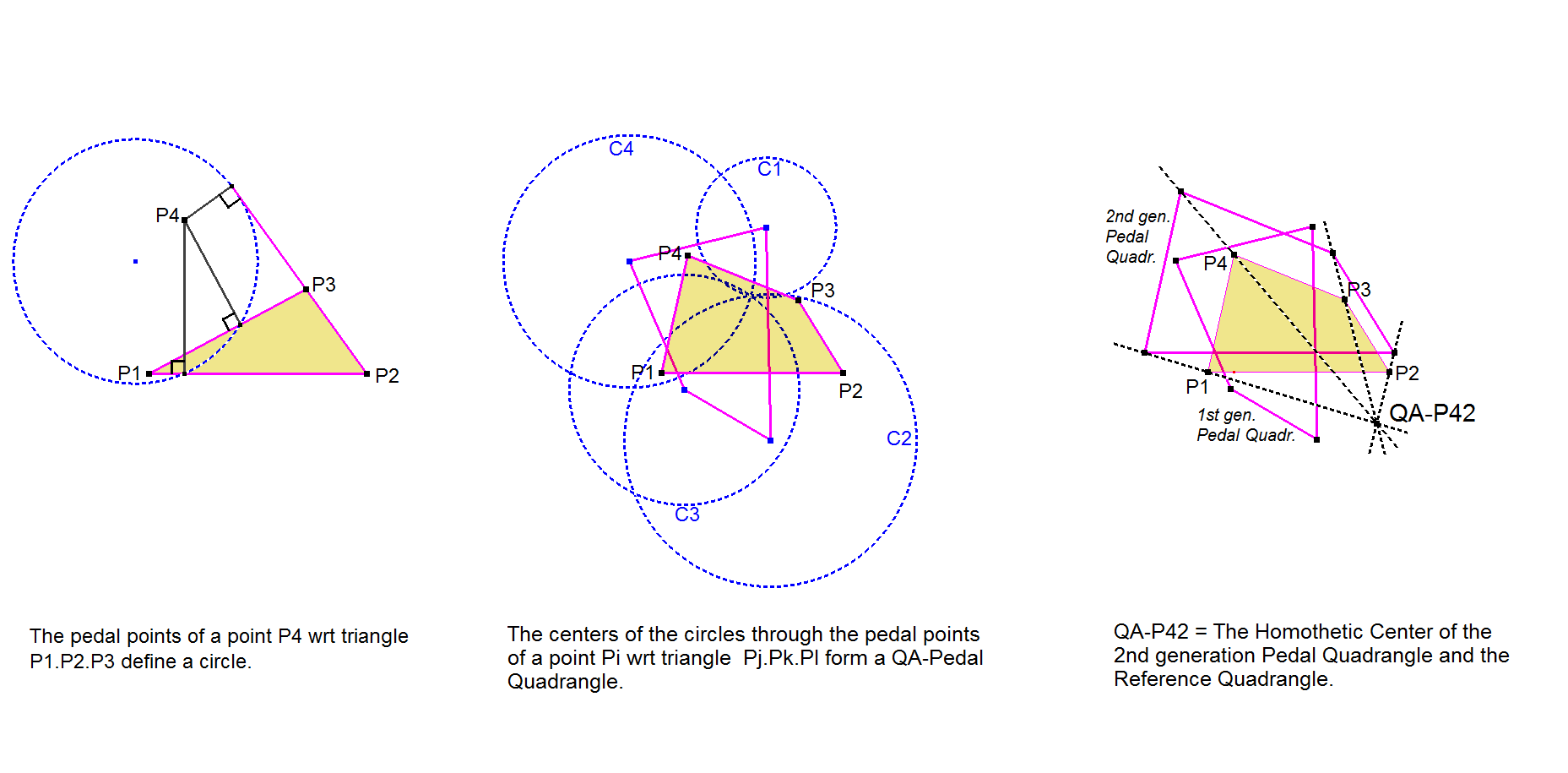
There is also a second major construction for this point.

The 4 centers of the circles through the pedal points of Quadrangle point Pi wrt Triangle Pj.Pk.Pl where (i,j,k,l) ∈ (1,2,3,4) form a QA-Pedal Quadrangle.

QA-P42 is the Homothetic Center of the 2nd generation QA-Pedal Quadrangle and the Reference Quadrangle.

The homothecy coefficient equals (2 cos α)² , where α is the angle formed by the asymptotes of QA-Co1 (this holds for convex quadrangles; a similar formula holds for the non-convex case). See [36], pages 348,349.

1st CT-Coordinate

a² q r (a² q r + 3 c² p q + 3 b² p r) + 2 p² (b² SC r² + c² SB q² + 2 S² q r)

1st DT-Coordinate

a⁴ (p² – q²) (p² – r²) + b² c² p² (p² + q² + r²)

+ b² p² (p² – q²) (b² – 2 a²) + c² p² (p² – r²) (c² – 2 a²)

Properties

• QA-P42 lies on these lines:
  • QA-P2.QA-P7(m : 1)
  • QA-P4.QA-P8(m : 1)
  • QA-P3.QA-Tf3(QA-P1)( n : 1)
  • QA-P12.QA-Tf3(QA-P11) ( n : 1)
  • QG-P5.QA-Tf3(QA-P7) ( n : 1)
  • QL-P26.QG-P12

• where (CT-coordinates):
• m = (2 (c² p q + b² p r + a² q r)² – 8 p q r S² (p + q + r))/ ( (c² p q + b² p r + a² q r)² + 12 p q r S² (p + q + r))
• n = ( (c² p q + b² p r + a² q r)² – 4 p q r S² (p + q + r))/ (-4 (c² p q + b² p r + a² q r)²)

• Triangle X.QA-P42.Y is similar to Triangle QA-Tf3(X).QA-P42.QA-Tf3(Y), so:

• Triangle QA-P2.QA-P42.QA-P11 is similar to Triangle QA-P4.QA-P42.QA-P12.
• Triangle QA-P7.QA-P42.QA-P11 is similar to Triangle QA-P8.QA-P42.QA-P12.

• Angle(QA-P2.QA-P42.QA-P11) = Angle(QA-P4.QA-P42.QA-P12).
• The QA-Orthopole(QA-Tf3) of QA-P42 is QA-P42.
• QA-P42 is the perspector of the QG-P12 Triple Triangle and the QL-P26 Triple Triangle.
• QA-P42 is collinear with QA-P1 and the reflection of QA-P4 in QA-P3. See [34], Eckart Schmidt, QFG-message #1666.

Estimated human page views: 566