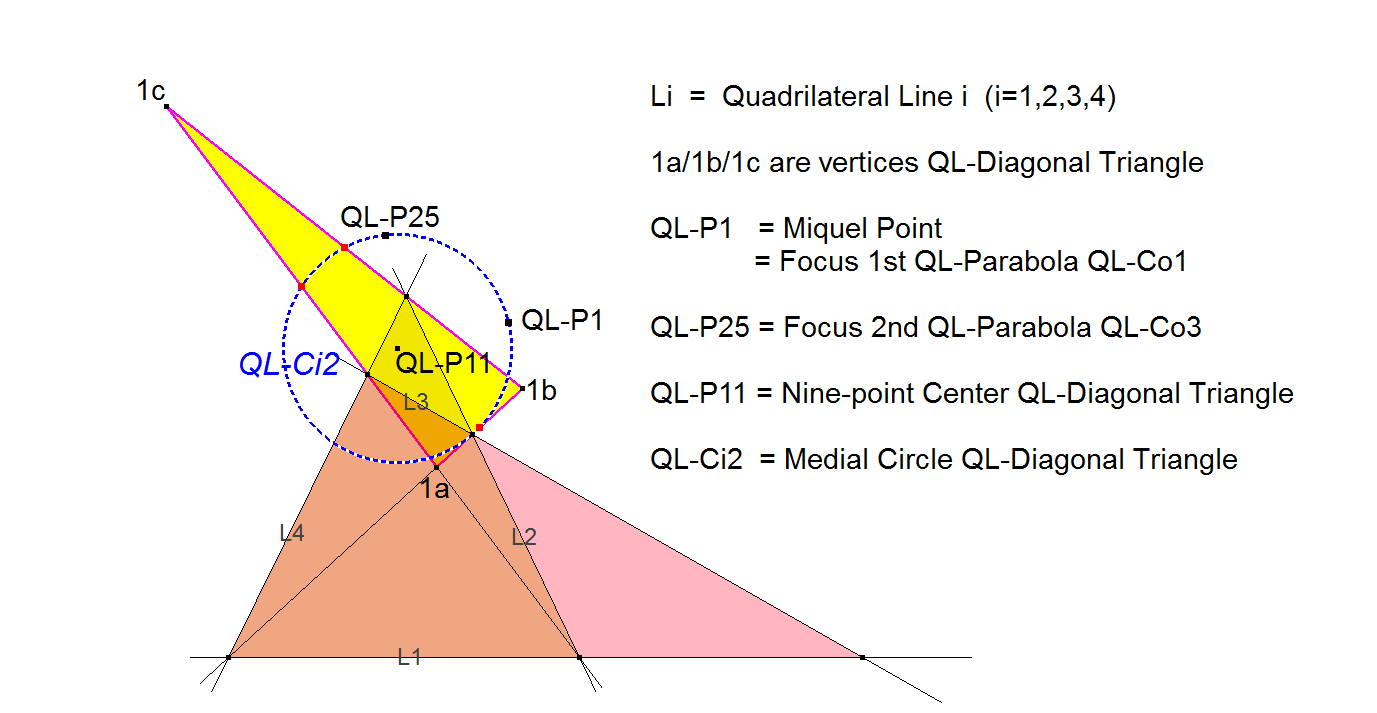
QL-Ci2: QL-Medial Circle Diagonal Triangle
QL-Ci2 is the Medial Circle of the QL-Diagonal Triangle (see paragraph QL-Tr1).
QL-P11 is its center.
Equation in CT-notation
l3 (m – n) (b m – c n)(b m + c n) x2
+ m3 (l – n) (a l – c n) (a l + c n) y2
+ n3 (l – m) (a l – b m) (a l + b m) z2
+ l m (( a2+b2-c2) l2 m2 + (c2-b2) l2 m n + (c2-a2) l m2 n – 2 c2 l m n2 + c2 l n3 + c2 m n3) x y
+ l n (( a2-b2+c2) l2 n2 + (b2-a2) l m n2 + (b2-c2) l2 m n – 2 b2 l m2 n + b2 m3 n+ b2 l m3) x z
+ m n ((-a2+b2+c2) m2 n2 + (a2-c2) l m2 n + (a2-b2) l m n2 – 2 a2 l2 m n + a2 l3 m + a2 l3 n) y z = 0
Radius2 of Circle in CT-notation
(a2 l2 – a2 l m – b2 l m + c2 l m + b2 m2)
* (a2 l2 – a2 l n + b2 l n – c2 l n + c2 n2)
* (b2 m2 + a2 m n – b2 m n – c2 m n + c2 n2)
* l2 m2 n2 / (16 Δ2 (l m – l n – m n)2 (l m + l n – m n)2 (l m – l n + m n)2)
where Δ = Area = 1/4 √[(a + b + c) (-a + b + c) (a – b + c) (a + b – c)]
Equation of Circle in DT-notation:
SA x (-x+y+z)+SB y (x-y+z)+SC (x+y-z) z = 0
Radius2 of Circle in DT-notation:
a2 b2 c2 / (16 S2)
Properties
- QL-P11 is the center of the Medial Circle.
- These points lie on QL-Ci2:
- The 2nd intersection point of QL-Ci2 and QL-Ci6 lies on QL-P8.QL-P17.QL-P25. See [34], Eckart Schmidt, QFG-message #1666.
- If we consider for the QL-inscribed conics the contact QA, their QA-P29 lie on QL-Ci2. See [66], Eckart Schmidt, QPG-message #1155.
Estimated human page views: 645
