nL-e-P1: nL-Morley’s EnnaDeltoid Center
Morley describes this point in his paper: Orthocentric properties of the Plane n-line (Ref-49).
The range of points nL-e-P1 in a 4-Line, 6-Line, 8-Line, 10-Line will be resp. 4L-n-p1, 6L-n-p2, 8L-n-p3, 10L-n-p4, etc.. See nL-n-pi points.
Schematically it shows (note the use of lower cases in items p0, p1, etc.):
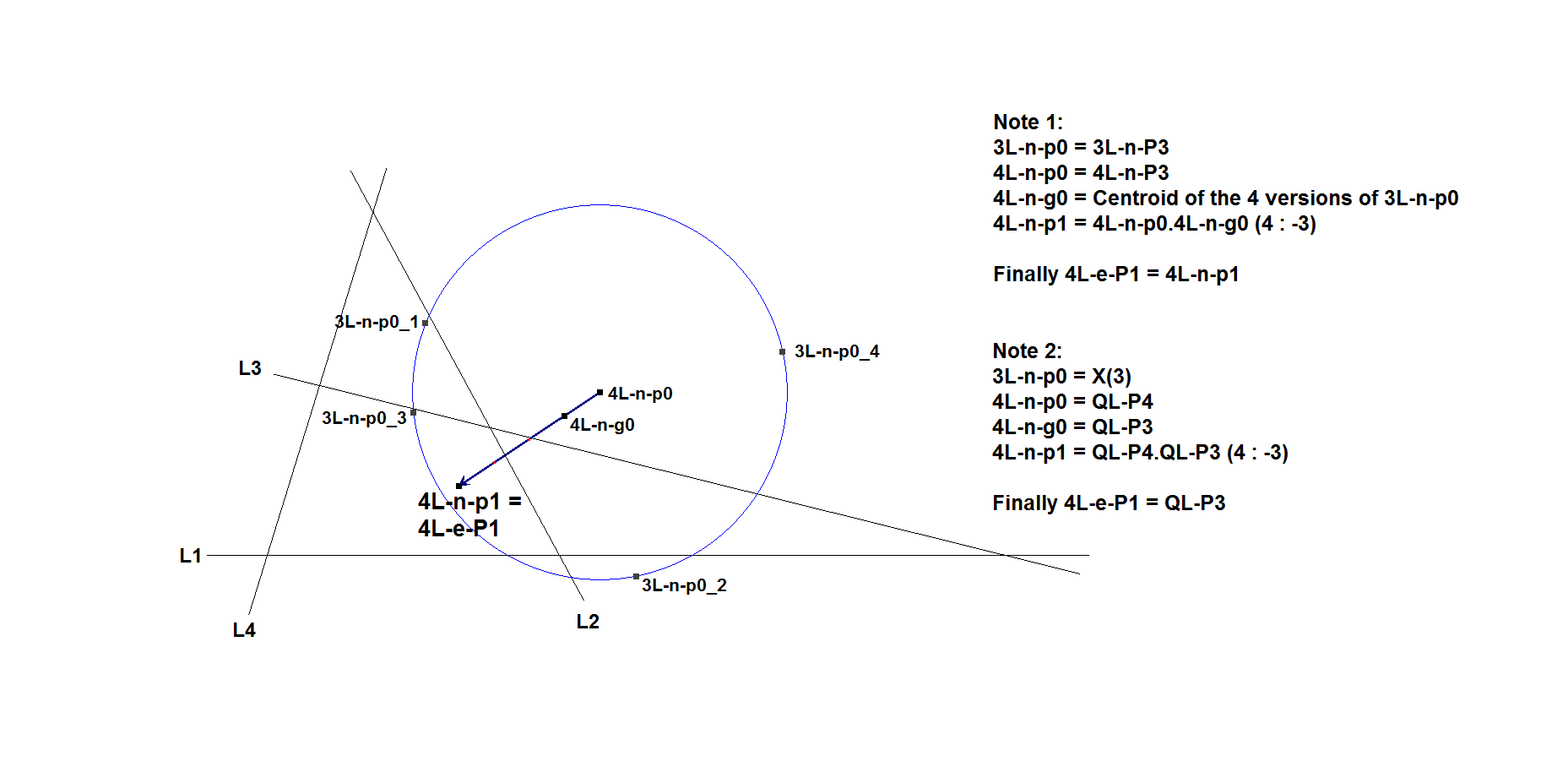
In a 4-Line:
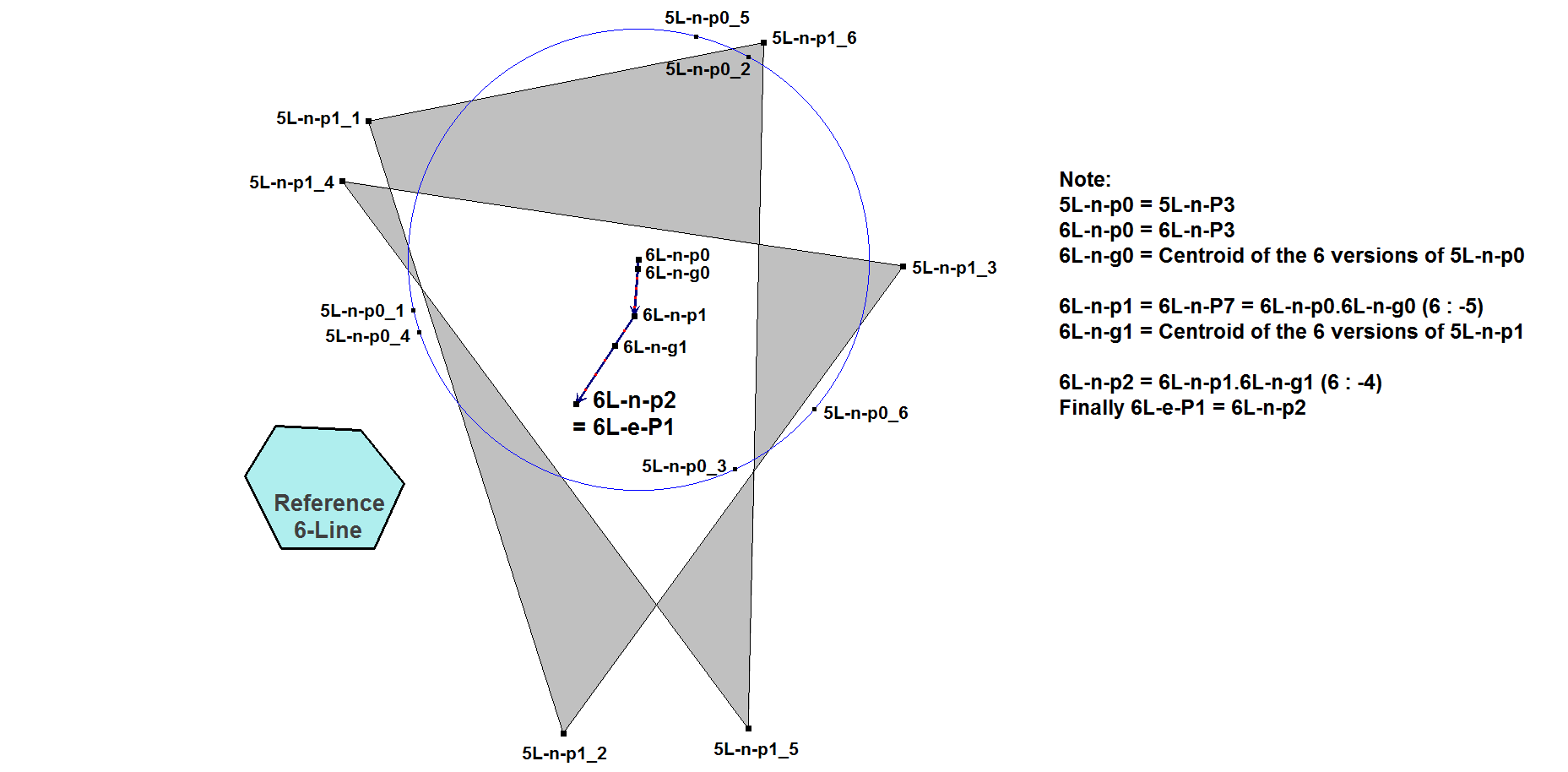
In a 6-Line:
In a 8-Line:
-
-
- The Circumcenter of the 8 points 7L-n-p0 is 8L-n-p0. = 8L-n-P3
- The Centroid of the 8 points 7L-n-p0 is 8L-n-g0.
- The Ratiopoint 8L-n-p0.8L-n-g0 (8:-7) is 8L-n-p1. = 8L-n-P7
- The Centroid of the 8 points 7L-n-p1 is 8L-n-g1.
- The Ratiopoint 8L-n-p1.8L-n-g1 (8:-6) is 8L-n-p2.
- The Centroid of the 8 points 7L-n-p2 is 8L-n-g2.
- The Ratiopoint 8L-n-p2.8L-n-g2 (8:-5) is 8L-n-p3. = 8L-e-P1
-
Etc.
Example of nL-e-P1 in a 4-Line
Example of nL-e-P1 in a 6-Line
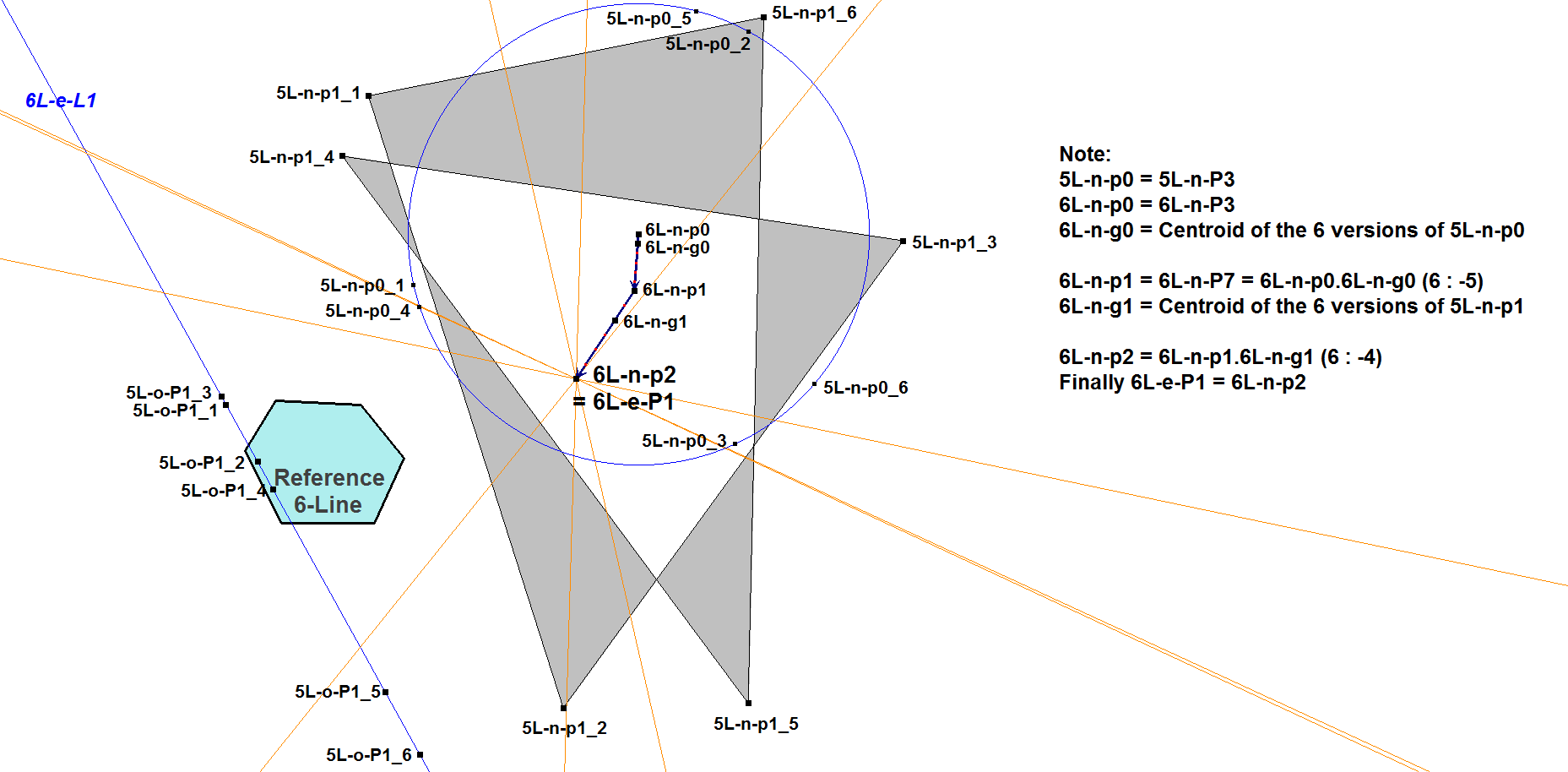
Example of nL-e-P1 in a 6-Line, where incidentally 6L-e-P1
is the common point of the perpendicular bisectors
of all 6 occurrences of 5L-o-P1_i.5L-n-P7_i (i=1, … , 6).
Correspondence with ETC/EQF
When n=4, then nL-e-P1 = QL-P3.
Properties
- nL-e-P1 can be constructed as the common point of the perpendicular bisectors (Level-up Construction nL-n-Luc2) of (n-1)L-o-P1. (n-1)L-n-pk, where m=n-1, k=(n-4)/2. See nL-n-pi points.
- nL-e-P1 can be constructed as the common point of the perpendicular bisectors (Level-up Construction nL-n-Luc2) of (n-1)L-n-ph. (n-1)L-n-pk, where m=n-1, h=(n-2)/2, k=(n-4)/2. See nL-n-pi points.
Estimated human page views: 452
