nP-n-P1 nP-MVP-Centroid
nP-n-P1 is the nL-Mean Vector Point of X(2), the Triangle Centroid.
In this method centroids (or other ETC-points) are successively constructed starting with n=3, then n=4 using the results of n=3, then n=5 using the results of n=4, etc.
See nP-n-Luc1 for a detailed description.
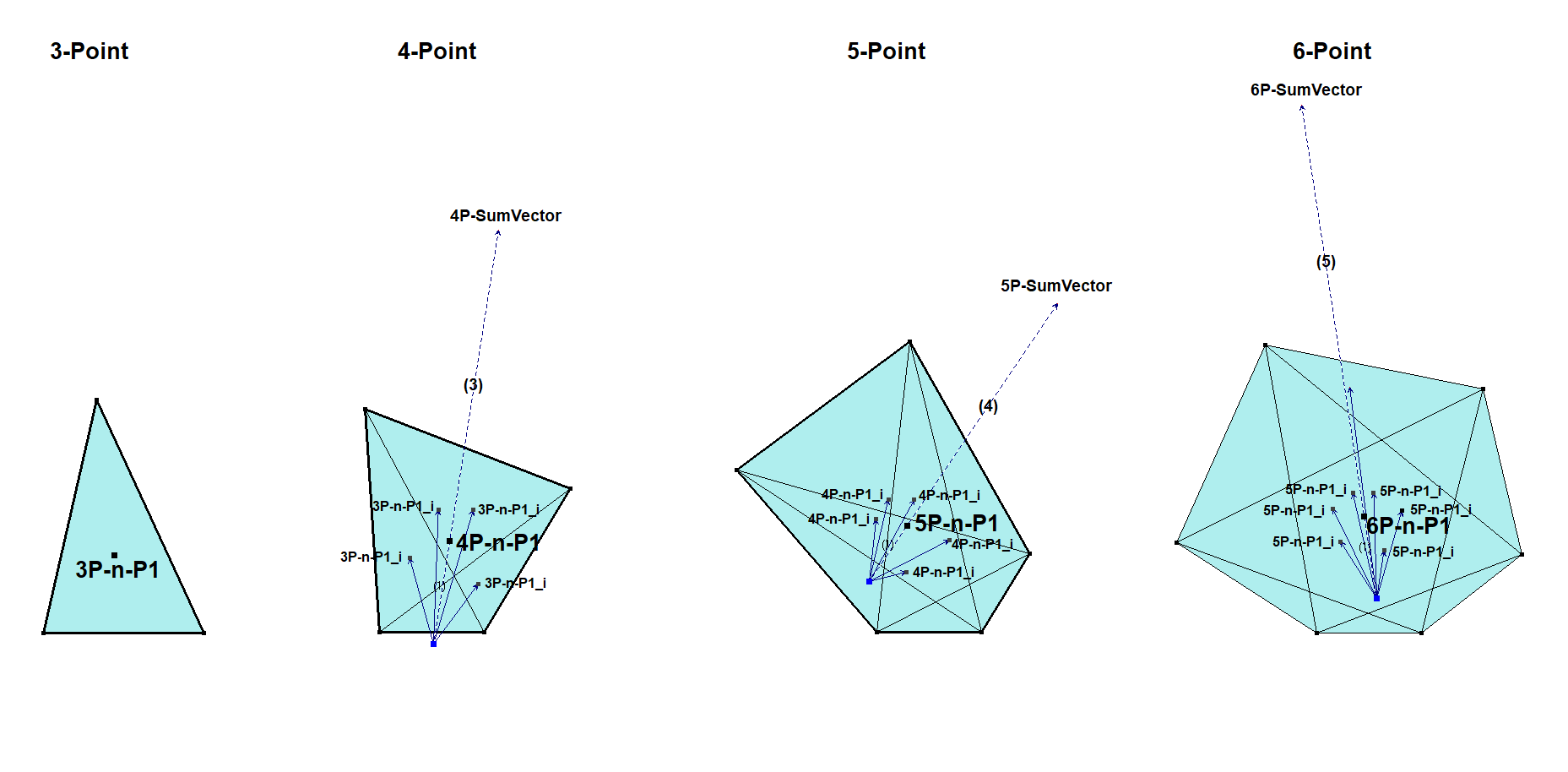
Another construction of nP-n-P1:
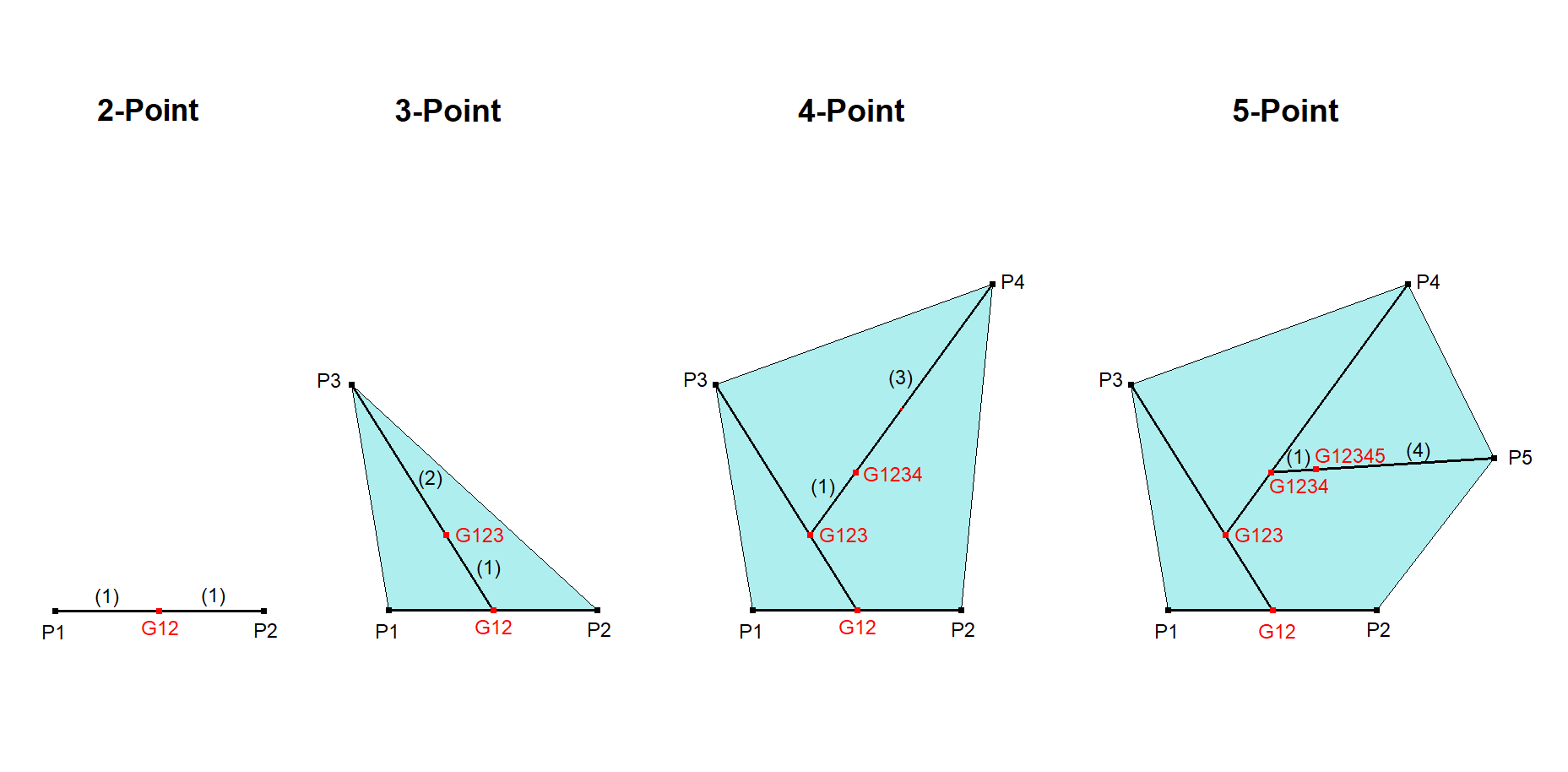
There is a simple “chain” for calculating centroids of consecutive n-Point figures.
1-Point Figure: G1 = Point P1
2-Point Figure: G12 = Midpoint (P1,P2) = point dividing G1,P2 with ratio 1 : 1
3-Point Figure: G123 = Centroid (P1,P2,P3) = point dividing G12,P3 with ratio 1 : 2
4-Point Figure: G1234 = Centroid (P1,P2,P3,P4) = point dividing G123,P4 with ratio 1 : 3
5-Point Figure: G12345 = Centroid (P1,P2,P3,P4,P5) = point dividing G1234,P5 with ratio 1 : 4
etc.
1st barycentric CT-coordinate
when P1=(1:0:0), P2=(0:1:0), P3=(0:0:1), P4=(p:q:r), P5=(P:Q:R), then:
nP-n-P1 = (q + r) (2 P + Q + R) + p (3 P + 2 Q + 2 R)
Correspondence with ETC/EQF
In a 3-Point:
- 3P-n-P1 = 3P-MVP Centroid = X(2)
- 3P-n-P2 = 3P-MVP Circumcenter = X(3)
- 3P-n-P3 = 3P-MVP Orthocenter = X(4)
- 3P-n-P4 = 3P-MVP Nine-point center = X(5)
In a 4-Point we find:
- 4P-n-P1 = 4P-MVP Centroid = QA-P1 (QA-Centroid)
- 4P-n-P2 = 4P-MVP Circumcenter = QA-P32 (Centroid Circumcenter Quadrangle)
- 4P-n-P3 = 4P-MVP Orthocenter = QA-P33 (Centroid Orthocenter Quadrangle)
- 4P-n-P4 = 4P-MVP Nine-point center = Midpoint (QA-P32,QA-P33)
Properties
- nP-n-P1, nP-n-P2, nP-n-P3 and nP-n-P4 are collinear on nP-n-L1. Their mutual distance ratios correspond with the mutual distance ratios from triangle centers X(2), X(3), X(4) and X(5).
- 5P-n-P1 is also the point that minimizes the sum of squared distances to the vertices of the Pentangle. See [34]. QFG #730, October 8, 2014 by Seiichi Kirikami.
- 5P-n-P1 is also the point that minimizes the sum of squared distances to all midpoints between vertices of the Pentangle. See [34]. QFG #730, October 8, 2014 by Seiichi Kirikami.
- 5P-n-P1 is also the point that minimizes the sum of squared distances to the Centroids of all Component Triangles of the Pentangle. See [34]. QFG #730, October 8, 2014 by Seiichi Kirikami.
Estimated human page views: 585
