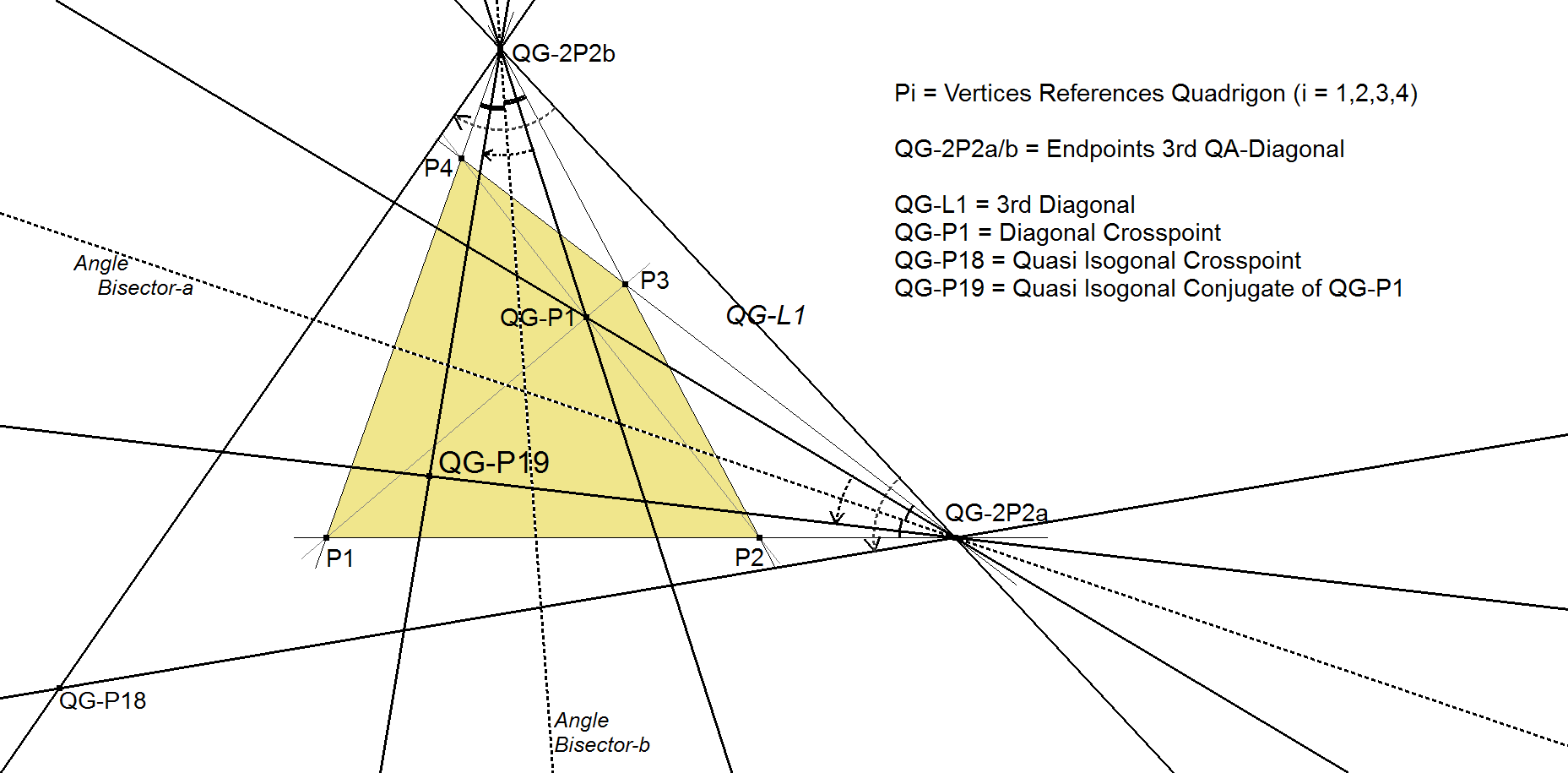
QG-P19: Quasi Isogonal Conjugate of QG-P1

QG-P19 is the intersection of the reflections of the two QA-DT-side lines unequal QG-L1 in the angle bisectors of the opposite sides of the quadrigon.

This point and its properties are found by Eckart Schmidt (December 12, 2012).

CT-Coordinates in 1^st QA-Quadrigon

(a² q r ((p + q) (b² p + a² q) r² + c² p q (p q – r²)) :

-p r (b⁴ p (p + q) r (q + r) – (a² – c²) q² (a² (p + q) r – c² p (q + r)) + b² q (-a² (p + q) (p – q – r) r + c² p (p + q – r) (q + r))) :

c² p q (c² p² q (q + r) + r (b² p² (q + r) + a² q (-p² + q r))))

DT-Coordinates in 1^st QA-Quadrigon

(-(a² + b² – c²) p² (c² q² + b² r²) :

(b² p² + a² q²) (c² q² + b² r²) :

(a² – b² – c²) (b² p² + a² q²) r²)

CT-Coordinates in 1^st QL-Quadrigon

(a² l (-a² (l – m) (l – n) + c² (l – n) (-m + n) + b² (l (m – n) + m (-2 m + n))) :

b² m (a² l² + c² n²) :

c² n (-a² (l – m) (l – n) + c² (l – n) (-m + n) + b² (l (m – n) + m (-2 m + n))))

DT-Coordinates in 1^st QL-Quadrigon

(-m² (a⁴ (l² – n²) + b² (b² – c²) (m² – n²) + a² (c² (-l² + n²) + b² (l² + m² + 2 n²))) :

2 b² c² (l² + m²) n² + c⁴ n² (-l² + n²) + 2 a² b² l² (m² + n²) + a⁴ (l⁴ – l² n²) + b⁴ (m⁴ – l² n²) :

m² (b⁴ (l² – m²) + c⁴ (l² – n²) – b² c² (2 l² + m² + n²) + a² (b² (-l² + m²) + c² (-l² + n²))))

Properties

• The QL-Tf1 image of QG-P19 is a point on QA-Ci1.
• QG-P19 is the QG-Tf2 image of QG-P1.
• QG-P19 is the QA-Tf2 image of the QG-P18.
• Let S_i = QG-P1, X_i = QG-P18 and Y_i = QG-P19 resp. in QA-Quadrigon-i (i=1,2,3). Now S_i.X_j ^ S_j.X_i = Y_k, S_i.Y_j ^ S_j.Y_i = X_k, X_i.Y_j ^ X_j.Y_i = S_k.
• The Triangles formed by the QA-versions of QG-P1, QG-P18 and QG-P19 are pairwise perspective triangles. Their centers of perspectivity are collinear.
• QA-P4 lies on the circle defined by the 3 QA-versions of QG-P19.
• QG-P19 is concyclic with QG2P2a, QG-2P2b, QA-P4 (the circle is the QL-Tf1 image of QA-Ci1).
• QG-P19 lies on QA-Cu7 (as 4^th intersection with the circle through QG2P2a, QG-2P2b, QA-P4).
• The altitudes of the Triangle formed by the 3 QA-versions of QG-P19 are concurrent in a point on QA-P12.QA-P24.
• The Polar (see [13], Polar) of QG-P19 wrt any circumscribed conic of the Reference Quadrigon is a line through QG-P18.
• The Triple Triangle of QG-P19 is perspective with all QA-Component Triangles (see QA-Tr-1 for Desmic Triple Triangles).

Estimated human page views: 522