QL-P30: Morley’s Second Circle Center
QL-P30 is the center of Morley’s Second Circle as described in [49].
Morley mentions in his paper how in an n-Line (system of n random lines) in a recursive way several centers can be constructed. In his terminology this Second Circle Center is the Ratiopoint nL-Center Circle Center : nL-Second Orthocenter ((n-2) : 1).
In EQF-terminology this is QL-P4.QL-P2 (2:1).
Morley’s Second Circle is the circle with center QL-P30 and with radius the QL-Ci3-radius / 3.
The external Homothetic Center of this Second Circle and Miquel Circle QL-Ci3 is QL-P2.
QL-P30 is used for constructing Morley’s Second Orthocenter in a 5-Line.
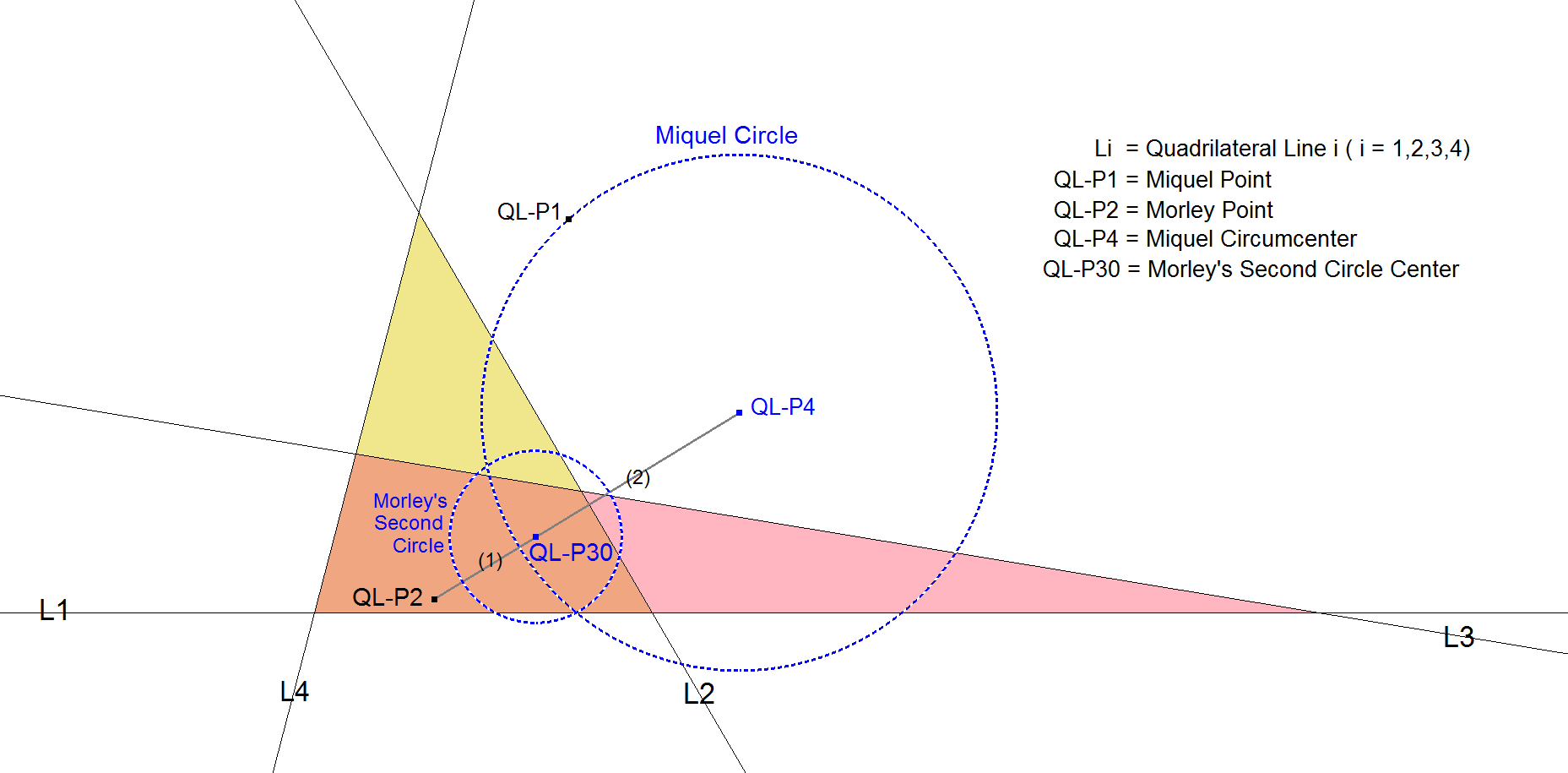
The Miquel Circle in a Quadrilateral is the equivalent of the circumcircle in a triangle.
Morley’s Second Circle in a Quadrilateral is the equivalent of the Nine-point Circle in a triangle.
1st CT-coordinate
+ a4 (m – n) (-l2 + m n) + b4 (l – 2 m) (l – n) (m – n) + c4 (l – m) (l – 2 n) (m – n)
– b2 c2 (m – n) (2 l2 – 3 l m – 3 l n + 4 m n) + a2 b2 (l – n) (2 m2 + l n – 3 m n) – a2 c2 (l – m) (l m – 3 m n + 2 n2)
Properties
- QL-P30 lies on these lines:
- QL-P30 is the center of Morley’s Second Circle.
- QL-P30 is used for the construction of 5L-Morley’s Second Orthocenter.
Estimated human page views: 646
