← Previous Next →

QL-P28: Circumcenter QL-X(186)-Quadrangle

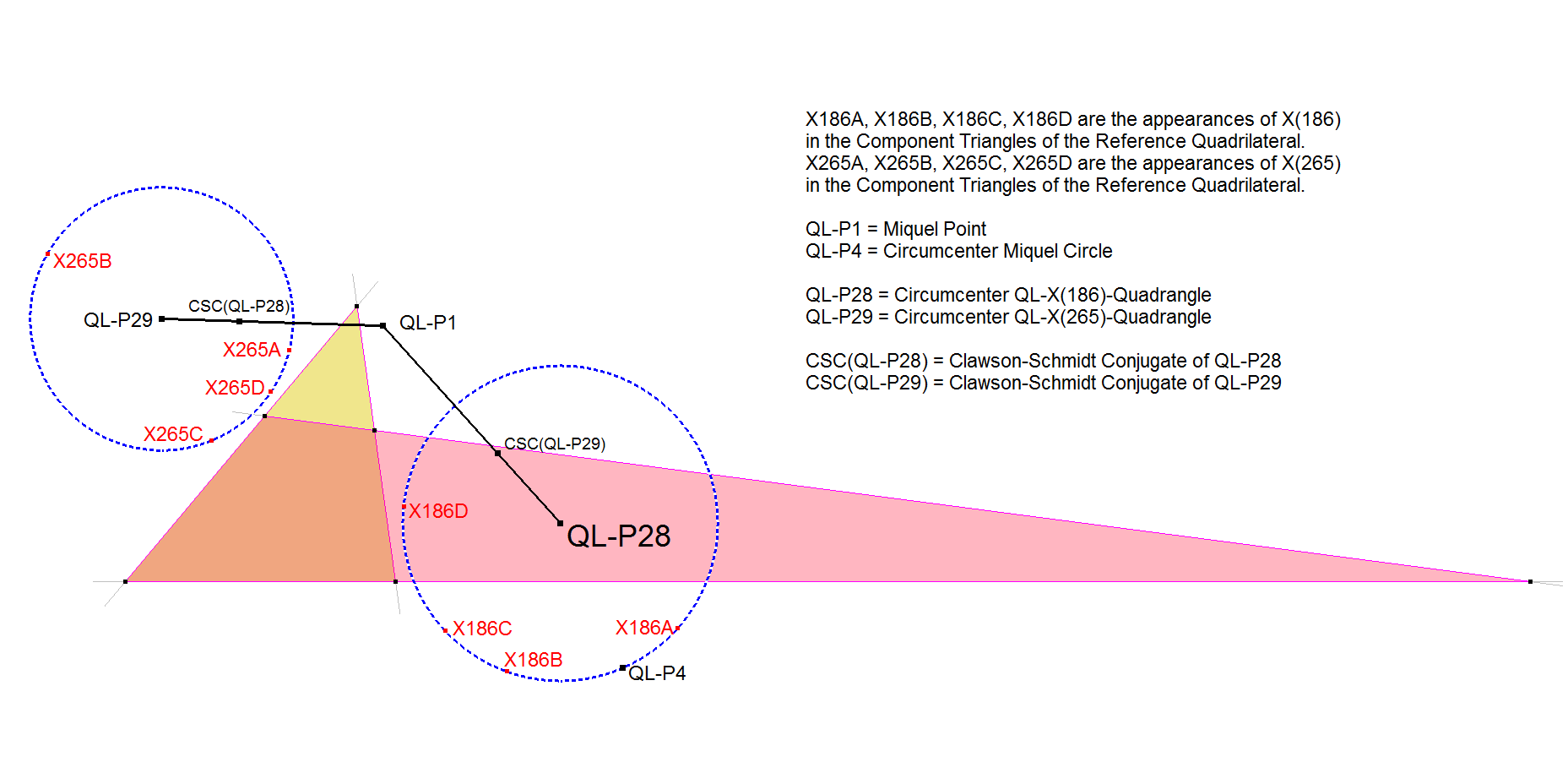
QL-P28 is the Circumcenter of the circle through the four X(186) points of the Component Triangles of the Reference Quadrilateral also called the QL-CT-versions of X(186).

X(186) is the Inverse of the Orthocenter X(4) in the circumcircle of a triangle.

See [12] for an explanation of ETC-points X(i).

See [33] Anopolis message # 409 for a discussion on this point.

There actually are 3 Triangle-points in ETC in the range X(1)-X(4000) for which their appearances in the Component Triangles of a Quadrilateral are concyclic: X(3), X(186), X(265). Only for X(4) these appearances are collinear in this range.

It’s remarkable that these points all relate to X(3) and X(4).

Infovisual QL-P28-infovisual-cvt-01.png
1st CT-coordinate

a2 (a6 (l – m) (l – n) (2 l – m – n) (m – n)

+ b6 (l3 m – 3 l2 m2 – m n (3 m2 – 3 m n + n2) + l (2 m3 + 3 m2 n – 3 m n2 + n3))

– c6 (l3 n – 3 l2 n2 – m n (m2 – 3 m n + 3 n2) + l (m3 – 3 m2 n + 3 m n2 + 2 n3))

+ b2 c4 ( 9 l m n2 – 3 l2 n (2 m + n) + l3 (m + 2 n) + m n (m2 – 3 m n – n2))

+ b4 c2 (-9 l m2 n – l3 (2 m + n) + 3 l2 m (m + 2 n) + m n (m2 + 3 m n – n2))

+ 3 a2 b4 (l – m) (l – n) (m – n) (m – n)

– 3 a2 c4 (l – m) (l – n) (m – n) (m – n)

+ a4 b2 (l3 (-3 m + 2 n) + m n (m2 + 3 m n – 3 n2) + 3 l2 (m2 + 2 m n – 2 n2) + 3 l n (-3 m2 + m n + n2))

– a4 c2 (l3 (2 m – 3 n) + 3 l m (m2 + m n – 3 n2) + m n (-3 m2 + 3 m n + n2) + l2 (-6 m2 + 6 m n + 3 n2))

+ a2 b2 c2 (m – n) (l3 + 9 l m n – 3 l2 (m + n) – 2 m n (m + n)))

1st DT-coordinate

+ a8 (l2 – m2) (l2 – n2) (m2 – n2) (5 l4 – l2 m2 – l2 n2 – 3 m2 n2)

+ b8 (l2 – m2) (l2 + 3 m2) (m – n)3 (m + n)3

+ c8 (l2 – n2) (l2 + 3 n2) (m – n)3 (m + n)3

– 4 b6 c2 l2 (l2 – m2) (m – n)3 (m + n)3

– 4 b2 c6 l2 (l2 – n2) (m – n)3 (m + n)3

+ 6 b4 c4 (l2 – m2) (l2 – n2) (m – n)3 (m + n)3

+ 6 a4 b4 (l2 – m2) (l2 – n2) (m2 – n2) (3 l2 m2 + m4 – l2 n2 – 3 m2 n2)

– 6 a4 c4 (l2 – m2) (l2 – n2) (m2 – n2) (l2 m2 – 3 l2 n2 + 3 m2 n2 – n4)

+ 4 a2 b6 (l2 – m2) (-4 l2 m6 + 4 l4 m2 n2 + l2 m4 n2 + 7 m6 n2 – 6 l2 m2 n4 – 6 m4 n4 + l2 n6 + 3 m2 n6)

– 4 a2 c6 (l2 – n2) (l2 m6 + 4 l4 m2 n2 – 6 l2 m4 n2 + 3 m6 n2 + l2 m2 n4 – 6 m4 n4 – 4 l2 n6 + 7 m2 n6)

+ 4 a6 c2 (l2 – n2) (2 l6 m2 +3 l4 m4 – l2 m6 + 2 l6 n2 – 13l4 m2 n2 + 6 l2 m4 n2 – 3 m6 n2 + 2 l4 n4 – l2 m2 n4 + 3 m4 n4)

– 4 a6 b2 (l2 – m2) (2 l6 m2 + 2 l4 m4 + 2 l6 n2 -13 l4 m2 n2 – l2 m4 n2 + 3 l4 n4 + 6 l2 m2 n4 + 3 m4 n4 – l2 n6 – 3 m2 n6)

– 4 a2 b4 c2 (-l4 m6 – 3 l2 m8 + 12 l6 m2 n2 – 18 l4 m4 n2 + 15 l2 m6 n2 + 3 m8 n2 – 21 l4 m2 n4 + 27 l2 m4 n4 – 18 m6 n4 + 4 l4 n6 – 3 l2 m2 n6 + 3 m4 n6)

+ 4 a2 b2 c4 (4 l4 m6 + 12 l6 m2 n2 – 21 l4 m4 n2 – 3 l2 m6 n2 – 18 l4 m2 n4 + 27 l2 m4 n4 + 3 m6 n4 – l4 n6 + 15 l2 m2 n6 – 18 m4 n6 – 3 l2 n8 + 3 m2 n8)

– 4 a4 b2 c2 (m2 – n2) (3 l6 m2 + 5 l4 m4 + 3 l6 n2 – 16 l4 m2 n2 – 3 l2 m4 n2 + 5 l4 n4 – 3 l2 m2 n4 + 6 m4 n4)

Properties


Estimated human page views: 454

Scroll naar boven