← Previous Next →

QL-Tf4: QL-Orthopole

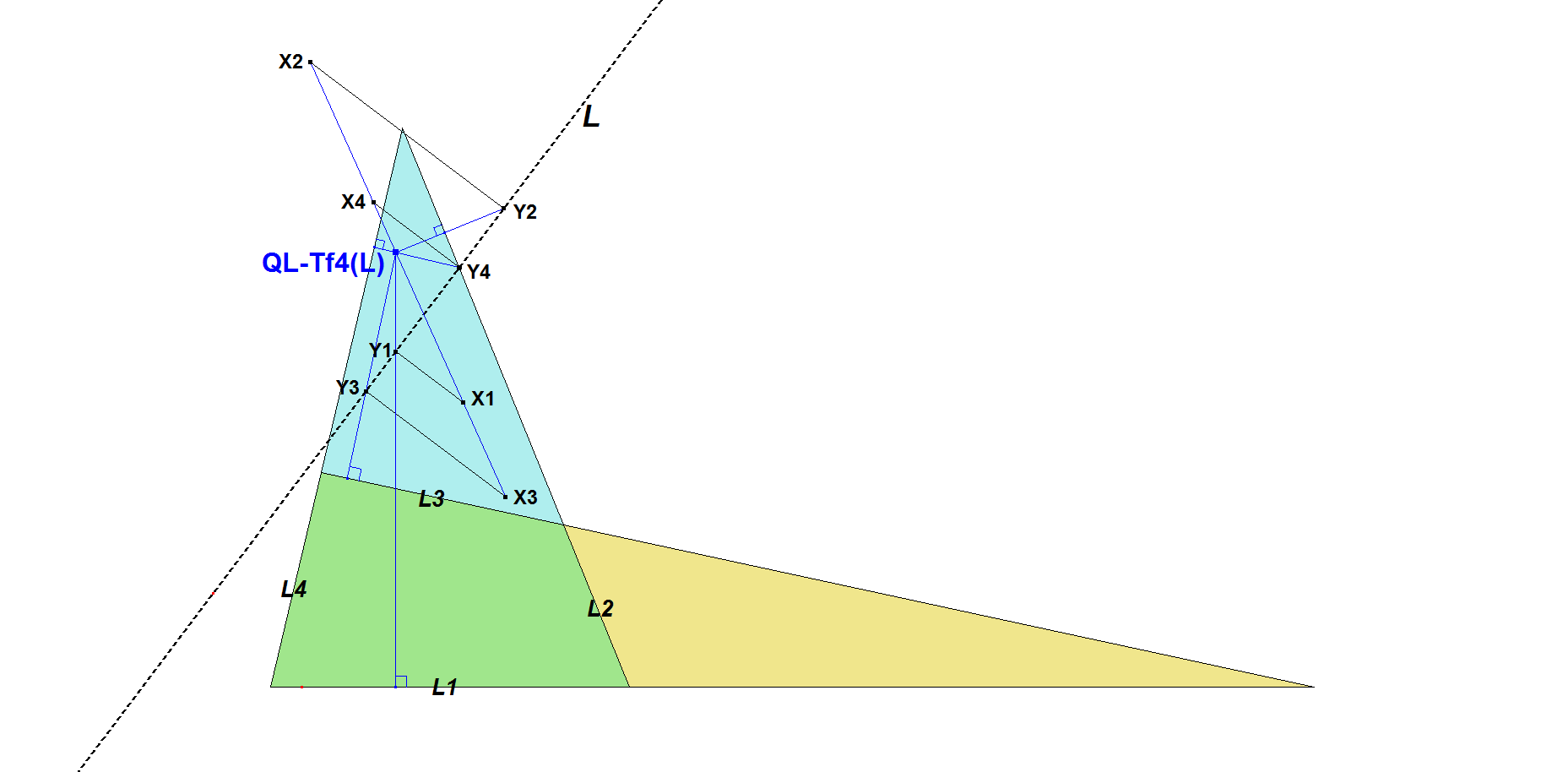
Let L1,L2,L3,L4 be a quadrilateral and let L be a random line.

Let X1 be the Orthopole (for definition see [13]) of L wrt triangle (L2,L3,L4). Let Y1 be the projection of X1 on L.

d1 is the line passing through Y1 perpendicular to L1. Similarly, we have the lines d2,d3,d4. Then d1,d2,d3,d4 are concurrent in a point P being called the QL-Orthopole, which is QL-Tf4(L). This transformation was first described by Tran Quang Hung. See[34], QFG#2062, #2064, #2070. For some examples see [34], QFG#2089.

Note that X1, X2, X3, X4 are collinear on a line being called the QL-Orthopolar Line, which is QL-Tf5(L). It is special that QL-Tf4(L) lies on QL-Tf5(L).

Infovisual QL-Tf4-infovisual-cvt-01.png
1st CT-coordinate of L(x:y:z)

2 m2 n T2 – l2 n T3 – 2 m n2 T4 + l2 m T5 – l m2 T6 + l n2 T7 + l m n T9

where:

T4 = -SB SC2 (x – y)2 y + SA2 (SB (x – 2 y) (y – z)2 + SC (x – y – z) (y – z)2) + SB2 SC (x – z) (x y – y2 – 2 x z + y z + z2) + SA (-SC2 (x – y)2 y + SB2 (-x + z) (y2 + x z – 2 y z) + SB SC (-x2 y + 4 x y2 – 3 y3 – x2 z – 4 x y z + 3 y2 z + 4 x z2 – 2 z3))

/ (SB x + SA y – c2 z) (SC x – b2 y + SA z)

T2 = T4 + SB (-y + z) + SC (-y + z)

T3 = 2 T4 + 2 SB (x – y) + 2 SC (x – z)

T5 = 2 T4 + 2 SC (x – y) + 2 SB (x – 2 y + z)

T6 = 2 T4 + 2 SC (x – y) – 2 SB (y – z)

T7 = 2 T4 + 2 SB (x – y)

T9 = 2 SC (x + y – 2 z) – 2 SB (x – 2 y + z)

Properties
  • The QL-Orthopoles of QL-L1, QL-L4 and QL-L5 are collinear on the Pedal Line QL-L3. See [34], QFG#2069.
  • The QL-Orthopoles of QL-L1 and QL-L3 are collinear with QL-P1. See [34], QFG#2069.
  • The QL-Orthopoles of QL-L2 and QL-L3 are collinear with QL-P21 on a line parallel to QL-P2.QL-P3. See [34], QFG#2069.
  • The QL-Orthopole of QL-L1 lies on the Newton Line QL-L1. See [34], QFG#2069.
  • The QL-Orthopole of QL-L3 lies on QL-P2.QL-P7. See [34], QFG#2069.
  • The QL-Orthopole of QL-L4 lies on QL-P2.QL-P3. See [34], QFG#2069.
  • The locus of QA-Orthopoles of the tangents at the QL-Inscribed Parabola QL-Co1 is the Steiner Line QL-L2. See [34], QFG#2070, #2089.
  • The QL-Orthopoles of lines through QL-P1 lie on QL-L3. See [34], QFG#2089.
  • The QL-Orthopoles of QL-L1-parallels lie on QL-L3. See [34], QFG#2089.
  • The QL-Orthopoles of QL-L1-perpendiculars lie on the QL-Cu1-asymptote. See [34], QFG#2089.
  • All lines with the same QL-Orthopole P have the same QL-Orthopolar, which is the QL-L1-perpendicular through P. See [34], QFG#2089.
  • The QL-Orthopoles of parallels L to a fixed line Lo lie on a perpendicular line L´ in a constant orientated distance d. Examples: 1) Lo = QL-L1, L´ = QL-L3, d = 0. 2) Lo = QL-L2, L´ = QL-Cu1-asymptote, d = distance of QL-L3 and QL-L2. See [34], QFG#2089.


Estimated human page views: 365

Scroll naar boven