← Previous Next →

QA-Cu7: QA-Quasi Isogonal Cubic

QA-Cu7 is the locus of all points Q for which the 3 Reflections of the line Q.Si in the angle bisectors of Si concur, where Si = ith vertex of the QA-Diagonal Triangle (i = 1,2,3). See also QG-Tf2 (Quasi Isogonal Conjugate).

The concurring point is also a point of the locus.

With the Reference Quadrangle as reference system this cubic can be seen as a circular isocubic invariant to the Involutary Conjugacy.

Construction: it is the locus of the intersection pint of the involutary conjugate of some line through QA-P4 and its perpendicular line through QA-P4 (note Eckart Schmidt). See QA-Cu-1, QA-Cubic Type 2.

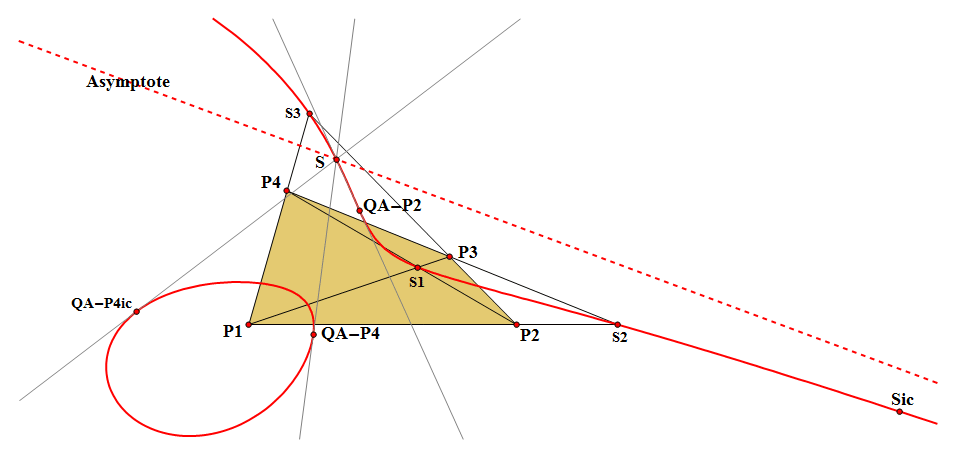
Infovisual QA-Cu7-infovisual-cvt-01.gif

QA-P4ic = Involutary Conjugate of QA-P4 = QA-P41,

Sic = Involutary Conjugate of S and the intersection of QA-P4.QA-P41 and perpendicular line in QA-P2 wrt QA-L2.

S is the intersection of QA-Cu7 and its asymptote

Equation CT-notation:

– b2 c2 p2 Tx (-q r x + p r y + p q z) x2

– a2 c2 q2 Ty ( q r x – p r y + p q z) y2

– a2 b2 r2 Tz ( q r x + p r y – p q z) z2

+ Txyz x y z

where:

Tx = c2 q2 – a2 q r + b2 q r + c2 q r + b2 r2,

Ty = c2 p2 + a2 p r – b2 p r + c2 p r + a2 r2

Tz = b2 p2 + a2 p q + b2 p q – c2 p q + a2 q2

Txyz = b2 c2 p4 + a2 c2 q4 – a2 (a2 – b2 – c2) q3 r + a2 (a2 + b2 + c2) q2 r2 – a2 (a2 – b2 – c2) q r3 + a2 b2 r4 + p3 (c2 (a2 + b2 – c2) q + b2 (a2 – b2 + c2) r) + p2 (c2 (a2 + b2 + c2) q2 + (a4 – a2 b2 – a2 c2 + 4 b2 c2) q r + b2 (a2 + b2 + c2) r2) + p (c2 (a2 + b2 – c2) q3 + (-a2 b2 + b4 + 4 a2 c2 – b2 c2) q2 r + (4 a2 b2 – a2 c2 – b2 c2 + c4) q r2 + b2 (a2 – b2 + c2) r3)

Equation DT-notation:

((b2 c2 p4 + a4 q2 r2) SA + p2 (c2 q2 + b2 r2) (S2 + SB SC)) (r2 y2 + q2 z2) x

+((a2 c2 q4 + b4 p2 r2) SB + q2 (c2 p2 + a2 r2) (S2 + SA SC)) (r2 x2 + p2 z2) y

+((c4 p2 q2 + a2 b2 r4) SC + (b2 p2 + a2 q2) r2 (S2 + SA SB)) (q2 x2 + p2 y2) z

+(a2 b2 (b2 p2 + a2 q2) r4 + a2 c2 q4 (c2 p2 + a2 r2) + b2 c2 p4 (c2 q2 + b2 r2)

+ 2 p2 q2 r2 (3 SA SB SC + S2 (SA + SB + SC))) x y z = 0

Properties
    • These points lie on QA-Cu7:
      • the vertices of the QA-Diagonal triangle,
      • QA-P2 (Euler-Poncelet Point),
      • QA-P4 (Isogonal Center)
      • QA-P41 (Involutary Conjugate of QA-P4)
      • the Involutary Conjugate of QA-P2 is the infinity point that represents the asymptote of the cubic.
      • the 3 QA-versions of QG-P18 (Quasi Isogonal Crosspoint)
      • the 3 QA-versions of QG-P19 (Quasi Isogonal Conjugate of QG-P1)
      • the circular points at infinity, which makes the cubic called circular.
    • The Asymptote is perpendicular to QA-L2 = QA-P2.QA-P4.
    • The Asymptote // 5th Point tangent of QA-P2 (see QA-Tf9).
    • The Involutary Conjugate of every point on the cubic also lies on the cubic.
    • The cubic is “self-involutary”.
    • The tangents at QA-P2, QA-P4 and QA-P4ic pass through the intersection point S of the asymptote and the cubic.
    • QA-Cu7 is the locus of all pairs of involutary conjugated points for which the Thales circle passes through QA-P4 (note Eckart Schmidt).
    • Any line though Pi, Pj (Pi,Pj are two of the four points P1, P2, P3, P4) intersects QA-Cu7 in one of the QA-DT-vertices and a pair of points (T1, T2).
    • Now (T1, T2) are harmonic conjugated with (Pi, Pj).
    • Let (Pk, Pl) be the other pair of points of the Quadrangle. Again Pk.Pl intersects QA-Cu7 in one of the QA-DT-vertices and a pair of points (U1, U2). Similarly (U1, U2) are harmonic conjugated with (Pk, Pl).
    • Now T1.U1 ^ T2.U2 as well as T1.U2 ^ T2.U1 are points lying on QA-Cu7.
    • The intersection points of QA-Cu7 and the 3 diagonals of the Reference Quadrangle (unequal the vertices of QA-DT) are collinear. These intersection points are the perspectors of the three pairs of QA-triangle versions of QG-P1.QG-P18.QG-P19. See [34], Eckart Schmidt, QFG#1263.
    • QA-Cu7 is a pivotal isogonal cubic wrt reference triangle QA-P2.QA-P4.QA-P41, the isogonal conjugacy and pivot in the point at infinity of a perpendicular of QA-L2 = QA-P2.QA-P4. See [34], Eckart Schmidt, QFG#1840.
Quasi Isogonal Conjugate:
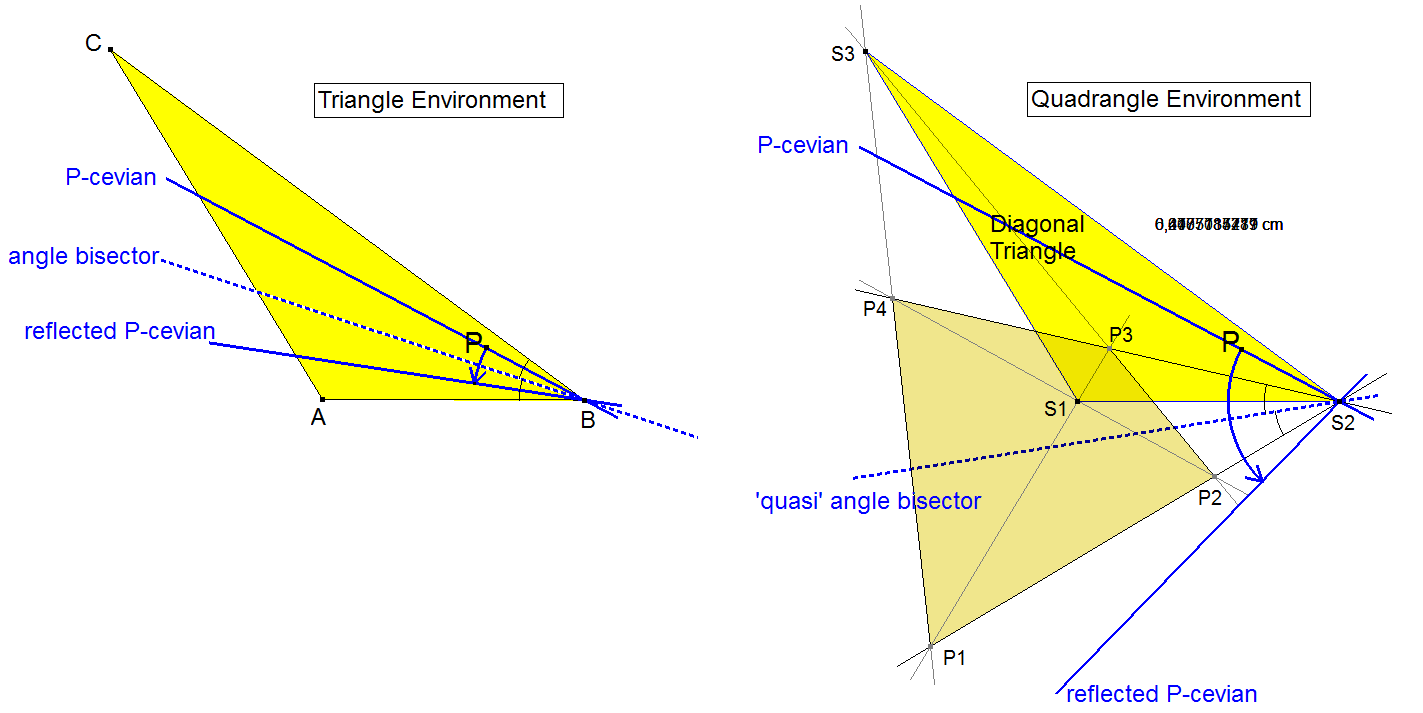
Infovisual QA-Cu7-infovisual-cvt-02.png
  • An Isogonal Conjugate is defined in the environment of a Triangle.
  • To construct an Isogonal Conjugate of a point P, reflections are made of the 3 P-cevians in the corresponding angle bisectors of the vertices of a triangle.
  • The reflected P-cevians concur in a point P*. P* is called the Isogonal Conjugate.
  • A Quasi Isogonal Conjugate (See QG-Tf2) is defined in the environment of a Diagonal Triangle of a Quadrangle.
  • To construct a Quasi Isogonal Conjugate of a point P, reflections are made of the 3 P-cevians in a Diagonal Triangle in the corresponding angle bisectors of the 3 pairs of opposite lines of a quadrangle.
  • The reflected cevians only concur in a point P* when P is situated on the Quasi Isogonal Cubic (QA-Cu7). P* is called the Quasi Isogonal Conjugate of P.


Estimated human page views: 706

Scroll naar boven