QA-Tf5: QA-Involution Center of 5^th point tangent

Let P (u : v : w) be a random point not on one of the connecting lines of the Reference Quadrangle. It is possible to construct a conic through P1, P2, P3, P4, P since a conic is defined by 5 points. The tangent to this conic at P is also called the 5^th Point tangent of P (see QA-Tf9). QA-Tf5 is the Involution Center of the QA-Line Involution (see QA-Tf1) occurring on this line.

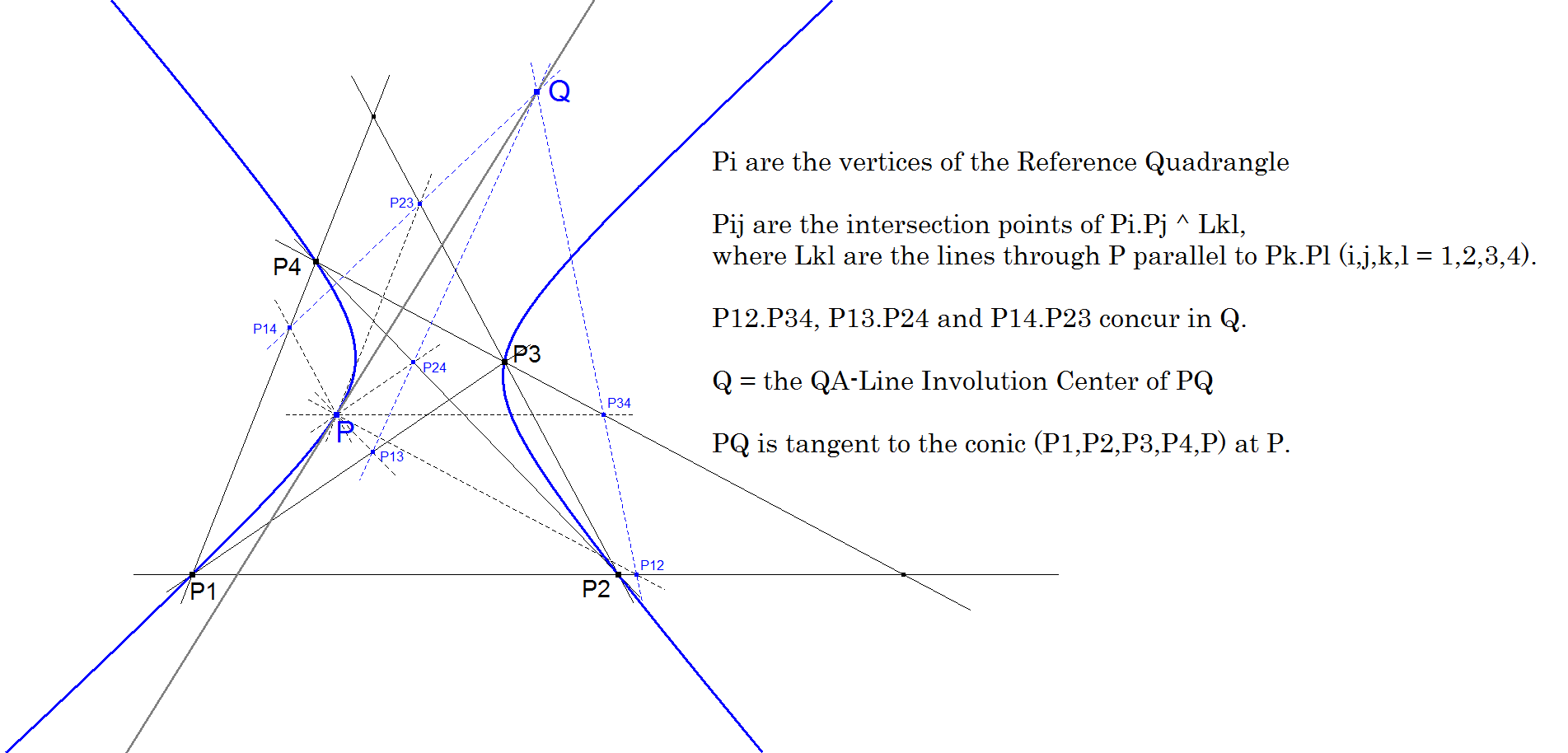
Construction

Seiichi Kirikami found an interesting construction of the Involution Center on the 5^th Point Tangent (see QA-Tf9) of random point P. See [34], QFG #1036, #1041.

Let L12, L13, L14, L23, L24, L34 be the lines through P parallel to P1P2, P1P3, P1P4, P2P3, P2P4, P3P4.

Let P12, P13, P14, P23, P24, P34 be the intersections of P1.P2 and L34, P1.P3 and L24, P1.P4 and L23, P2.P3 and L14, P2.P4 and L13, P3.P4 and L12 respectively.

P12P34, P13P24 and P14P23 concur in a point Q, being the Involution Center of the 5^th point Tangent at P.

Coordinates QA-Involution Center of 5^th Point tangent in CT-notation:

( u (+q r u² – p r u v – p q u w – p q v w – p r v w) :

v (-q r u v + p r v² – p q u w – q r u w – p q v w) :

w (-p r u v – q r u v – q r u w – p r v w + p q w²) )

Coordinates QA-Involution Center of 5^th Point tangent in DT-notation:

( r² u² v + q² u² w + p² v w (2 u + v + w) :

r² u v² + p² v² w + q² u w (u + 2 v + w) :

q² u w² + p² v w² + r² u v (u + v + 2 w) )

Properties

• f(P) = Midpoint (P , QA-Tf2(P))
• f(QA-P1) = f(QA-P20) = QA-P22
• f(QA-P6) = f(QA-P30) = QA-P6.QA-P30 ^ QA-P11.QA-P38
• QA-Tf5(P) is infinite when P lies on the nine point conic QA-Co1 (See [34], QFG#1038 by Francisco Javier).
• QA-Tf5 transforms a generic line r into a cubic with a Doublepoint on r (See [34], QFG#1040 by Benedetto Scimemi).
• QA-Tf5 transforms a quadrangle side into itself (the same line, counted 3 times) and therefore:
  • QA-Tf5 fixes the four quadrangle vertices; other fixed points are at infinity, i.e. the 6 sides directions
  • QA-Tf5 transforms a side of the diagonal triangle into the 3 sides of its own medial triangle
  • QA-Tf5 transforms the 9-point conic into the line at infinity (as noted by Francisco Xavier); in particular :
    • a side midpoint goes into that side direction
    • a diagonal point is singular; as a limit, it goes into the midpoint of its own opposite side
    • QA-P3 goes into the direction QA-P3.QA-P4; QA-P2 normal to QA-P2.QA-P4. (See [34], QFG#1040 notes by Benedetto Scimemi).

Estimated human page views: 595