← Previous Next →

QA-Tf12: QA-Pedal Point

The QA-Pedal Point is defined as follows.

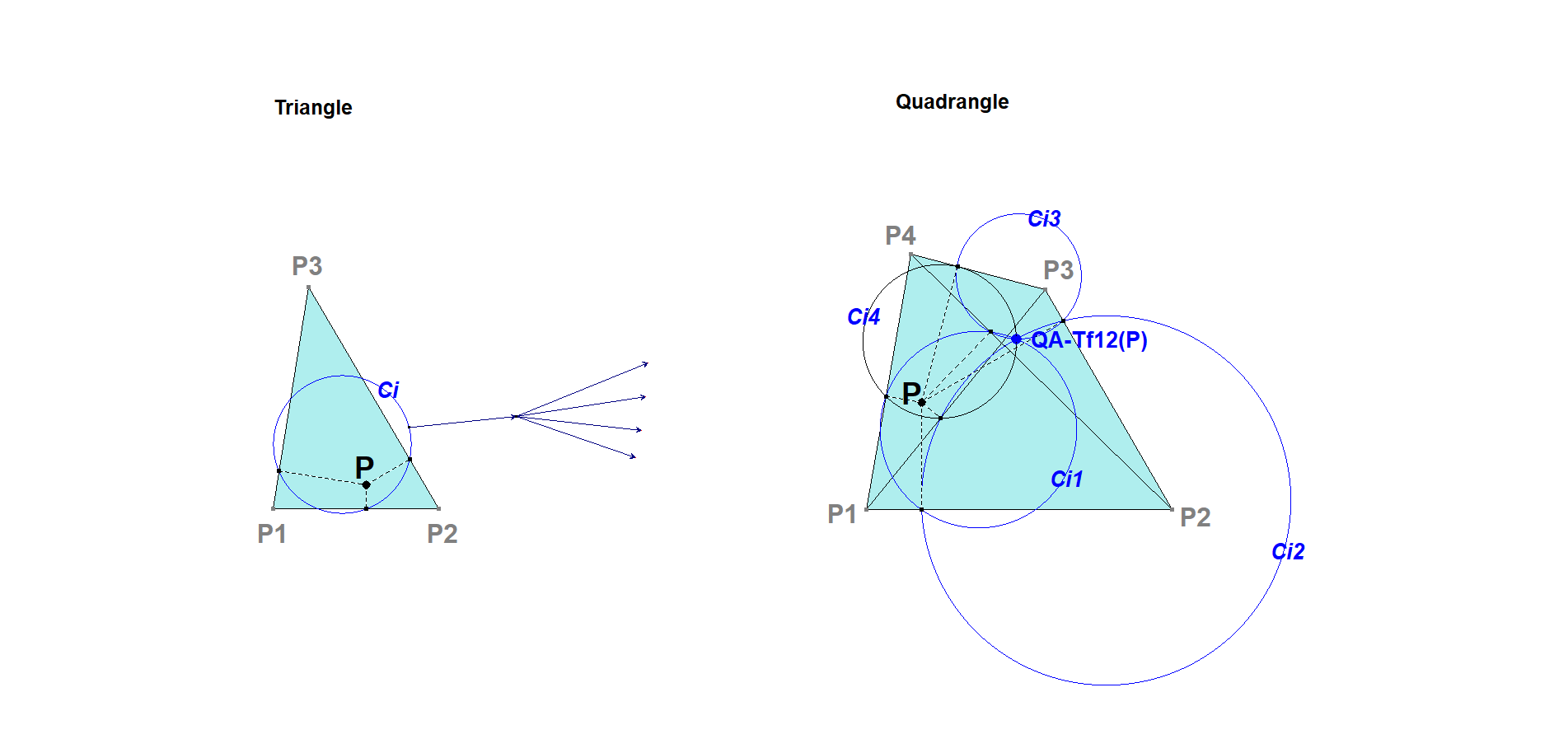
The 3 Pedal Points of P wrt a Triangle define a Pedal Circle Ci.

In a Quadrangle the 4 Pedal Circles Ci (denoted as Ci1, Ci2, Ci3, Ci4) of the Component Triangles intersect at a common point being the QA-Pedal Point.

For more information and background on this transformation see [34], QFG-messages #1218, #1219, #1222, #1223, #1231, #1232, #2759.

Infovisual QA-Tf12-infovisual-cvt-01.png
1st CT-coordinate of QA-Tf12[(x:y:z)]:

p (r y – q z) (c2 (2 b2 p + a2 q + b2 q – c2 q) r x3 y + c2 (a2 p + b2 p – c2 p + 2 a2 q) r x2 y2 + b2 q (-2 c2 p – a2 r + b2 r – c2 r) x3 z – 2 p (a2 c2 q + b2 c2 q – c4 q – a2 b2 r + b4 r – b2 c2 r) x2 y z + (-2 a2 c2 p q + a4 p r – b4 p r + 2 b2 c2 p r – c4 p r + a4 q r – a2 b2 q r + a2 c2 q r) x y2 z – b2 q (a2 p – b2 p + c2 p + 2 a2 r) x2 z2 + (-a4 p q + b4 p q – 2 b2 c2 p q + c4 p q + 2 a2 b2 p r – a4 q r – a2 b2 q r + a2 c2 q r) x y z2 – a2 p (a2 q – b2 q + c2 q – a2 r – b2 r + c2 r) y2 z2)

Properties
  • Every point on a side of a Quadrangle is transformed in the projection point on the opposite side of the Quadrangle.
  • QA-Tf12 has the vertices of the Diagonal Triangle as fixed poins. See [34], QFG#1231.
  • QA-P4 is transformed into QA-P2. See [34], QFG#1219.
  • Not only QA-P4 is transformed into QA-P2, but all points of the QA-Orthogonal Hyperbola QA-Co2. See [34], QFG#1231.
  • QA-Tf12(P) = CO-Tf3-1(P) wrt the conic(P1,P2,P3,P4,P), where P1, P2,P3, P4 are the vertices of the Reference Quadrangle (personal mail Benedetto Scimemi and see [34], QFG#1252).
  • QA-P12 can be generalized as the transformation nP-e-Tf1 in an n-Point (system of n reference points). It matches with nP-e-Tf1 when n=4. See [34], QFG#2759.
  • Given a Pentangle {P1, P2, P3, P4, P5}.
  • Let A1 = QA-Tf14 (P1) wrt {P2,P3,P4,P5}; similarly we define A2, A3, A4, A5.
  • Let B1 = QA-Tf12 (P1) wrt {P2,P3,P4,P5}; similarly we define B2, B3, B4, B5.
  • Then two pentangle {P1,P2,P3,P4,P5}, {A1,A2,A3,A4,A5} are inversely similar and the two pentangles {A1,A2,A3,A4,A5}, {B1, B2, B3, B4. B5} are homothetic with the center of the circumconic of {P1,P2,P3,P4,P5} as homothetic center. The circumconics of {P1,P2,P3,P4,P5}, {A1,A2,A3,A4,A5} and {B1, B2, B3, B4. B5} are similar and share the same center. See Vu Thunh Tang at [59b].
  • The locus of QA-Tf6(L) wrt a pencil of lines L through a random point P is a circle. It is the same circle as occurs in the construction of QA-Tf3. Its center is QA-Tf3(P). QA-P2 and QA-Tf12(P) lie on this circle. The point QA-Tf12(P) is identical with 5P-s-Tf3(P) of Pentangle P1.P2.P3.P4.P. The angle deviation of L through P is transformed in a doubled angle deviation of QA-Tf6(P) on this circle in the opposite direction.


Estimated human page views: 252

Scroll naar boven