QA-Co2: QA-Orthogonal Hyperbola

Since an Orthogonal Hyperbola (OH) is determined by 4 points there is only one Orthogonal Hyperbola defined by the vertices of a quadrangle.

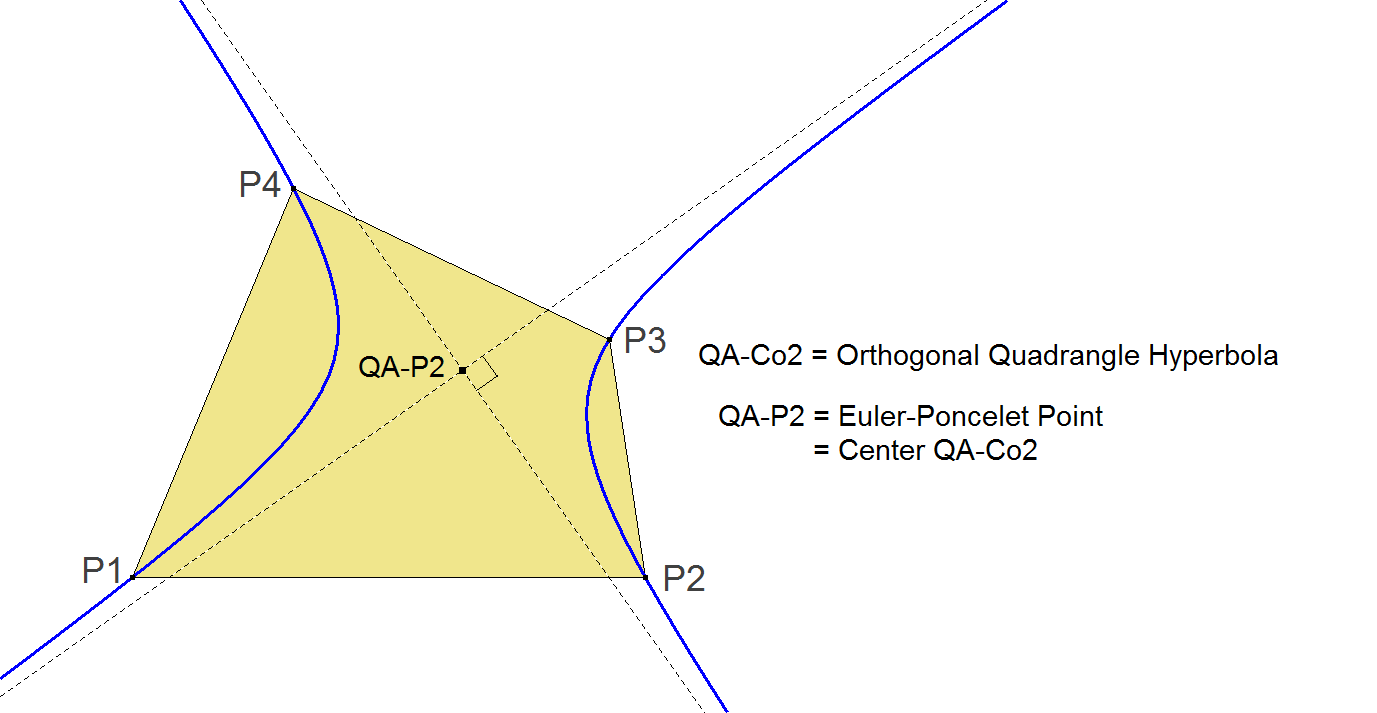
QA-Co2 is the unique Orthogonal Hyperbola defined by the vertices of the reference quadrangle.

Equation CT-notation:

(S_A x – S_B y) p q z + (S_B y – S_C z) q r x + (S_C z – S_A x) p r y = 0

Equation DT-notation:

(b² r² – c² q²) x² + (c² p² – a² r²) y² – (b² p² – a² q²) z² = 0

Properties

• The orthocenters of all QA-Component Triangles lie on this hyperbola.
• QA-P2 (Euler-Poncelet Point) is the center of the QA-Orthogonal Hyperbola.
• The asymptotes of the QA-Orthogonal Hyperbola are parallel to:
  • the axes of the Nine-point Conic (QA-Co1)
  • the axes of the Gergonne-Steiner Conic (QA-Co3)
  • the reflection axes of the QA-Orthopole Transformation (QA-Tf3).
• The incenter and the excenters of the QA-Diagonal Triangle (QA-Tr1) lie on QA-Co2. This property can be found at [36] page 347, as well as at [28] page 100, theorem 4.2. See also [11], Hyacinthos message # 21130 of Floor van Lamoen.
• The QA-Diagonal Triangle (QA-Tr1) is self-polar wrt QA-Co2.
• QA-P11.QA-P41 intersects QA-Co2 on QA-Cu1. See [34], Eckart Schmidt, QFG-message #1666.
• The vertices of the anticevian triangle (wrt QA-Tr1) of any point of QA-Co2 also will be resident on QA-Co1. See [34], Eckart Schmidt, QFG-message #1666.
• Let P be on QA-Co2 and X, Y its reflections in PiPj and PkPl, then the circumcircles of XPiPj and YPkPl intersect in the reflection of P in QA-P2. See [34], Eckart Schmidt, QFG-message #1666.

Estimated human page views: 580