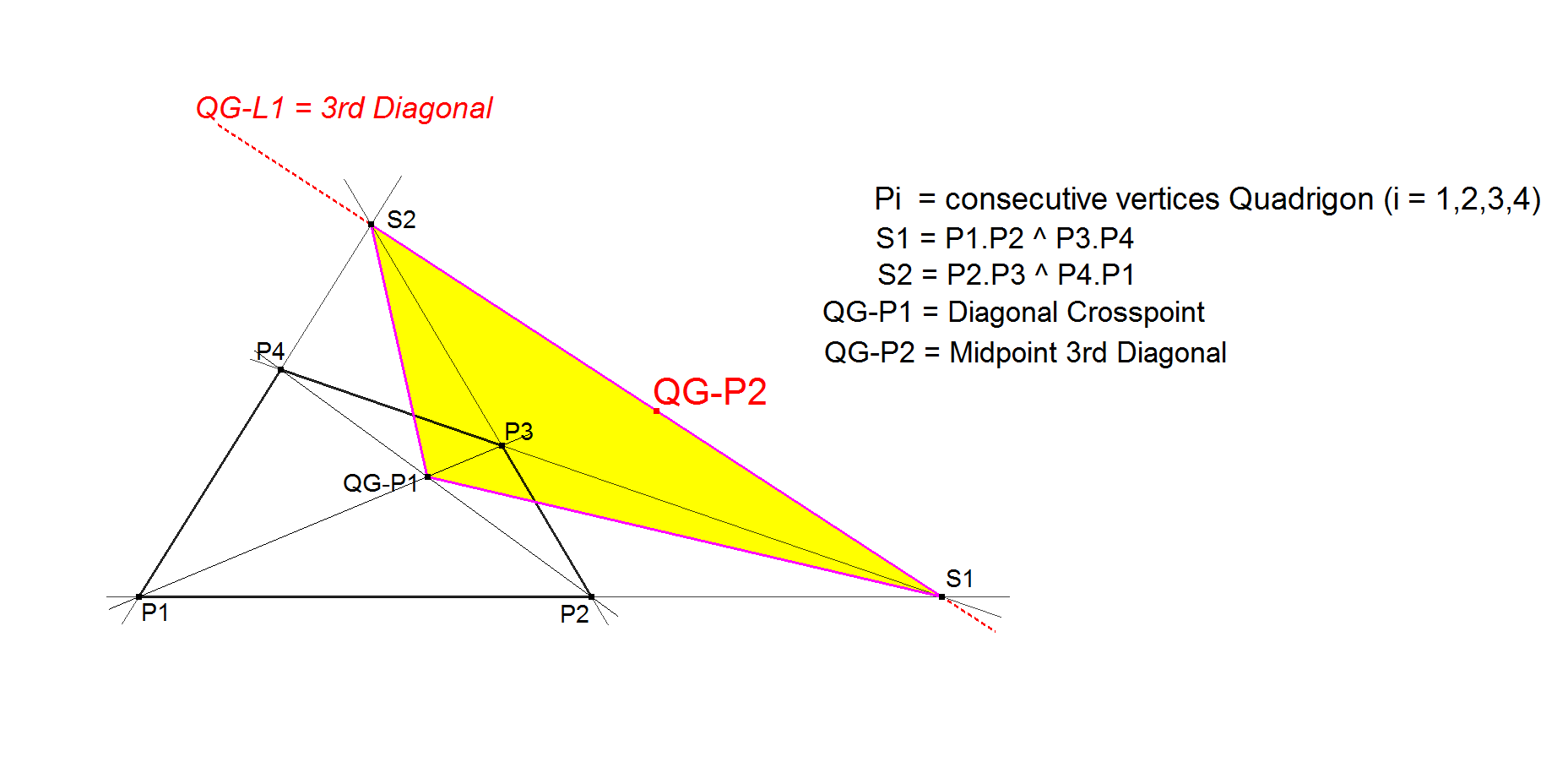
QG-P2 Midpoint 3rd QA-Diagonal
We use this terminology:
- A “QA-Quadrigon” is a Quadrigon seen as the Component of a Quadrangle.
- A “QL-Quadrigon” is a Quadrigon seen as the Component of a Quadrilateral.
The 3rd Diagonal of a QA-Quadrigon is the same line as the 3rd Diagonal of a QL-Quadrigon. However the Midpoint of a QA-Quadrigon is different from the Midpoint of a QL-Quadrigon.
QG-P2 is the Midpoint of the segment on the 3rd Diagonal of a QA-Quadrigon limited by the intersection points with the 3rd Diagonals of the 2 other Component QA-Quadrigons.
Construction
Let S1 = P1.P2 ^ P3.P4 and S2 = P2.P3 ^ P4.P1.
QG-P2 = the Midpoint of S1 and S2.
CT-Coordinates QG-P2 in 3 QA-Quadrigons:
(p (2 p + q + r) : q (p + r) : r (p + q))
(p (q + r) : q (p + 2 q + r) : r (p + q))
(p (q + r) : q (p + r) : r (p + q + 2 r))
CT-Coordinates QG-P2 in 3 QL-Quadrigons:
(m – n : -n : m)
(n : n – l : -l)
(-m : l : l – m)
CT-Area of QG-P2-Triangle in the QA-environment:(equals ¼ x area QL-Diagonal Triangle)
p q r Δ /(2 (p + q) (p + r) (q + r))
CT-Area of QG-P2-Triangle in the QL-environment:(points are collinear)
0
—
DT-Coordinates QG-P2 in 3 QA-Quadrigons:
(1 : 0 : 1)
(0 : 1 : 1)
(1 : 1 : 0)
DT-Coordinates QG-P2 in 3 QL-Quadrigons:
(n2 : 0 : – l2 )
(0 : n2 : -m2)
(m2 : – l2 : 0)
DT-Area of QG-P2-Triangle in the QA-environment:(equals ¼ area QA-Diagonal Triangle)
S / 8
DT-Area of QG-P2-Triangle in the QL-environment:(points are collinear)
0
Properties
- QG-P2 lies on these lines:
- QG-P2 is the fourth harmonic point of QG-P12 (Inscribed Harmonic Conic Center) on the Newton Line (QL-L1) wrt the midpoints of the diagonals (note Eckart Schmidt).
- The triangle formed by the 3 QA-Versions of QG-P2 is the medial triangle of the QA-Diagonal Triangle.
- The 3 QL-Versions of QG-P2 are 3 points on the Newton Line QL-L1 with centroid QL-P12. See [66], QPG-message#1271.
- The Polar (see [13], Polar) of QG-P2 wrt QG-Co1 as well as QG-Co2 is the line QG-P1.QG-P3.
- The circle defined by the 3 versions of QG-P2 (QA-Ci2) in a Quadrangle is incident with QA-P17, QA-P29, QA-P36 and the foci of the QA-parabolas (QA-2Co1).
- The Triple Triangle of QG-P2 is perspective with all QA-Component Triangles (see QA-Tr-1 for Desmic Triple Triangles).
Estimated human page views: 704
