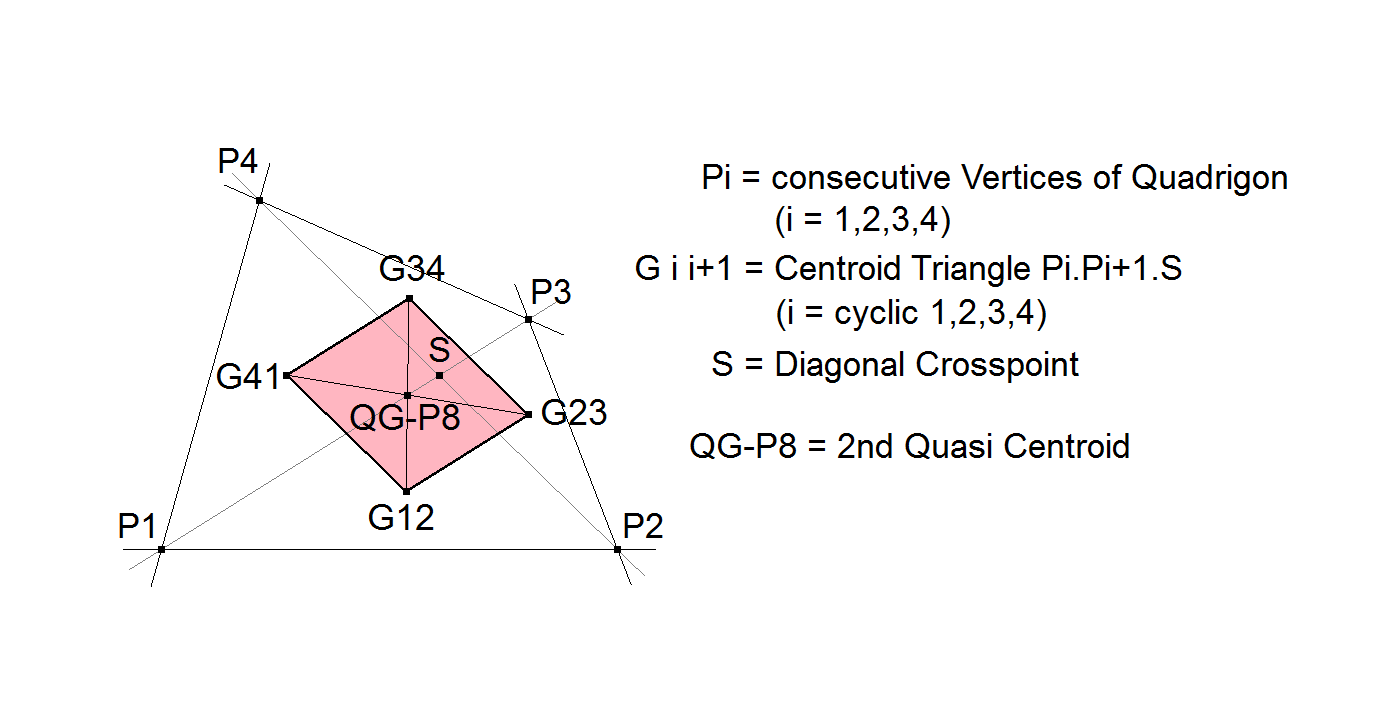
QG-P8 2^nd Quasi Centroid

Let P1.P2.P3.P4 be a Quadrigon and let S be its Diagonal Crosspoint QG-P1.

Let Gi i+1 = Centroid of Triangle Pi.Pi+1.S (i = cyclic sequence 1,2,3,4) .

Now is G12.G23.G34.G41 a parallelogram.

The sides of this parallelogram are parallel to the diagonals of the Reference Quadrigon.

QG-P8 is the Center of this parallelogram.

CT-Coordinates QG-P8 in 3 QA-Quadrigons:(only coordinates of 1^st Quadrigon point are given)

(-12 p⁶ – 9 p⁵ q – 63 p⁵ r – 39 p⁴ q r – 135 p⁴ r² – 66 p³ q r² – 150 p³ r³ – 54 p² q r³ – 90 p² r⁴ – 21 p q r⁴ – 27 p r⁵ – 3 q r⁵ – 3 r⁶ : -3 p⁶ – 6 p⁵ q – 18 p⁵ r – 30 p⁴ q r – 45 p⁴ r² – 60 p³ q r² – 60 p³ r³ – 60 p² q r³ – 45 p² r⁴ – 30 p q r⁴ – 18 p r⁵ – 6 q r⁵ – 3 r⁶ : -3 p⁶ – 3 p⁵ q – 27 p⁵ r – 21 p⁴ q r – 90 p⁴ r² – 54 p³ q r² – 150 p³ r³ – 66 p² q r³ – 135 p² r⁴ – 39 p q r⁴ – 63 p r⁵ – 9 q r⁵ – 12 r⁶)

CT-Coordinates QG-P8 in 3 QL-Quadrigons (only coordinates of 1^st Quadrigon point are given)

((m – n) (-l² m + 2 l m² + l² n – 5 l m n + 4 m² n) :

-l² m² + 5 l² m n – 4 l m² n – 4 l² n² + 5 l m n² – m² n² :

-(l – m) (4 l m² – 5 l m n + 2 m² n + l n² – m n²))

CT-Area of QG-P8-Triangle in the QA-environment:

2 p q r Δ / (9 (p + q) (p + r) (q + r))(equals 1/9 area QA-Diagonal Triangle)

CT-Area of QG-P8-Triangle in the QL-environment:(equals 2/9 area QL-Diagonal Triangle)

8 l² m² n² Δ / (9 (l m – l n – m n) (l m + l n – m n) (l m – l n + m n))

–

DT-Coordinates QG-P8 in 3 QA-Quadrigons (only coordinates of 1^st Quadrigon point are given)

(2 p² (p²-q²-r²) : (p²-r²)² -4 q² (p²+r²)+3 q⁴ : 2 r² (-p²-q²+r²))

DT-Coordinates QG-P8 in 3 QL-Quadrigons (only coordinates of 1^st Quadrigon point are given)

(m² (m²-n²) : -2 (l²-m²)(m²-n²)+(-m⁴+l² n²) : m² (-l²+m²))

DT-Area of QG-P8-Triangle in the QA-environment

S/18(equals 1/9 area QA-Diagonal Triangle)

DT-Area of QG-P8-Triangle in the QL-environment:(equals 2/9 area QL-Diagonal Triangle)

S/9

Properties

• QG-P8, QG-P9, QG-P10, QG-P11 are collinear on QG-L5, the 2^nd QG-Quasi Euler Line.
• QG-P1, QG-P4, QG-P8, QG-P15, QA-P1 are collinear on QG-L3, the QG-Centroids Line.
• QG-P8 is the Centroid of the 2^nd QG-Quasi Diagonal Triangle: QG-Tr2.
• QG-P8 is the Midpoint of QG-P1 and QG-P4.
• QG-P8 is the Reflection of QG-P4 in QA-P1 (QA-Centroid).
• QG-P8 lies on this line: QA-P26.QL-P12 (-2 : 3) (Eckart Schmidt, July, 2012).
• The QG-P8 Triangle in the QA-environment and the QA-Diagonal Triangle are homothetic with Homothetic Center QA-P1.
• The area of the QA-versions of QG-P8 = 1/9 of the area of the QA-Diagonal Triangle.
• The area of the QL-versions of QG-P8 = 2/9 of the area of the QL-Diagonal Triangle.
• QA-P26 is the Centroid of the Triangle formed by the 3 QA-versions of QG-P8.
• QL-P15 is the Centroid of the Triangle formed by the 3 QL-versions of QG-P8.
• QG-P8 is the Kirikami Center (QG-P15) of the Quadrigon formed by the Centroids of the Component Triangles of the Quadrigon (Eckart Schmidt, August 24, 2012).
• Let Gi be the Centroids of the Component Triangles Pj.Pk.Pl of the Reference Quadrigon. Now QG-P8 is the Diagonal Crosspoint of the Quadrigon formed by the Midpoints(Pi, Gi) (Eckart Schmidt, September 18, 2012).
• QG-P8 is the Centroid of the Triangle QG-P1.QA-P25.QA-P26 (all Centroid related points).

Estimated human page views: 648