← Previous Next →

QG-P13: Circumscribed Harmonic Conic Center

The Circumscribed Harmonic Conic Center is the Center of the circumscribed Harmonic Conic QG-Co2. This conic touches the sidelines of the projective circumscribed Quadrigon in the vertices of the Reference Quadrigon.

See picture below.

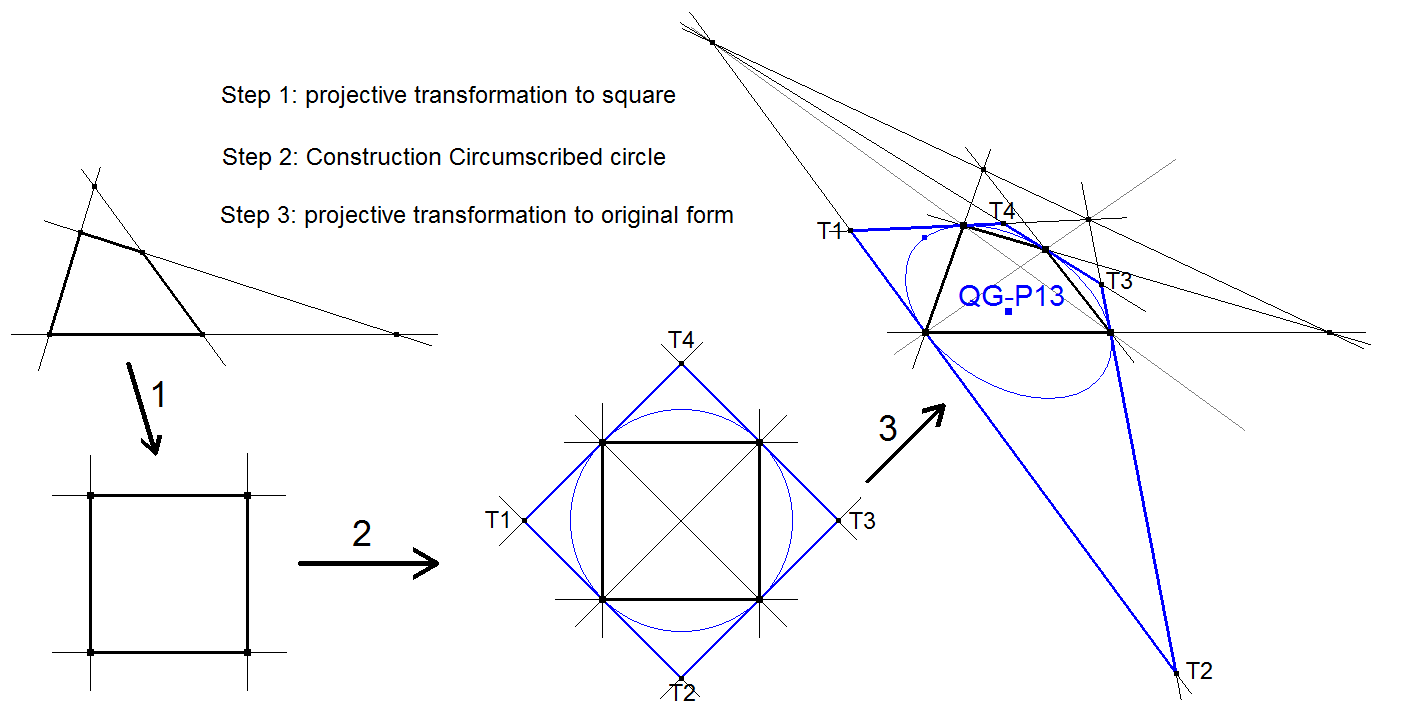
Infovisual QG-P13-infovisual-cvt-01.png
CT-Coordinates QG-P13 in 3 QA-Quadrigons

(2p (2p+q+r) : q (2p+q-r) : r (2p – q+r))

( p (p+2q -r) : 2q (p+2q+r) : r (-p+2q+r))

( p (p -q+2r) : q (-p+q+2r) : 2r ( p+q+2r))

CT-Coordinates QG-P13 in 3 QL-Quadrigons

(m n (l m + l n + m n) : l n (-3 l m + l n + m n) : l m (l m – 3 l n + m n))

(m n (-3 l m + l n + m n) : l n (l m + l n + m n) : l m (l m + l n – 3 m n))

(m n (l m – 3 l n + m n) : l n (l m + l n – 3 m n) : l m (l m + l n + m n))

CT-Area of QG-P13–Triangle in the QA-environment

54 p q r (p + q) (p + r) (q + r) Δ

/ (((q – r)2 + 4 p (p + q + r)) ((p – r)2 + 4 q (p + q + r)) ((p – q)2 + 4 r (p + q + r)))

CT-Area of QG-P13–Triangle in the QL-environment

16 l2 m2 n2 (lm-ln-mn) (lm+ln-mn) (lm-ln+mn) Δ

/ ((l2m2+l2n2+m2n2+2lmn(l+m-3n)) (l2m2+l2n2+m2n2+2lmn(l-3m+n))

(l2m2+l2n2+m2n22lmn(-3l+m+n)))

–

DT-Coordinates QG-P13 in 3 QA-Quadrigons

( – p2 : 2q2 : 2 r2)

(2 p2 : -q2 : 2 r2)

(2 p2 : 2q2 : – r2)

DT-Coordinates QG-P13 in 3 QL-Quadrigons

(-m2 n2 : l2 n2 : l2 m2)

( m2 n2 : -l2 n2 : l2 m2)

( m2 n2 : l2 n2 : -l2 m2)

DT-Area of QG-P13–Triangle in the QA-environment

-27 S p2 q2 r2 / (2 (-p2+2 q2+2 r2) (2 p2+2 q2-r2) (2 p2-q2+2 r2))

DT-Area of QG-P13–Triangle in the QL-environment

-2 S l4 m4 n4 / ((-l2 m2+l2 n2+m2 n2) (l2 m2+l2 n2-m2 n2) (l2 m2-l2 n2+m2 n2))

Properties
  • QG-P13 lies on these lines:
  • QG-P13 is the intersection of lines from an intersection of a diagonal with the 3rd diagonal and midpoint of the other diagonal (note Eckart Schmidt).
  • The triangle formed by the 3 QA-versions of QG-P13 is perspective with the triangle formed by the 3 QA-versions of QG-P1 (the QA-Diagonal Triangle).
  • Their Perspector is QA-P16 (QA-Harmonic Center).
  • The triangle formed by the 3 QL-versions of QG-P13 is perspective with the QL-Diagonal Triangle. Their Perspector is QL-P13 (QL-Harmonic Center).
  • The circumcenter of the triangle formed by the 3 QL-versions of QG-P13 is a point on QL-L6 (Quasi Ortholine).
  • QG-P13 lies on the Nine-point Conic QA-Co1.
  • So the vertices of the triangle formed by the 3 QA-versions of QG-P13 lie on the Nine-point Conic QA-Co1.
  • The Involutary Conjugate (QA-Tf2) of QG-P13 is the infinity Point of the line QG-P1.QG-P2.
  • QG-P13= the QL-DT-Trilinear Pole of the QA-DT-Trilinear Polar of QG-P14 (Eckart Schmidt, October 13, 2012). For definition Trilinear Pole and Polar see [13].


Estimated human page views: 516

Scroll naar boven