← Previous Next →

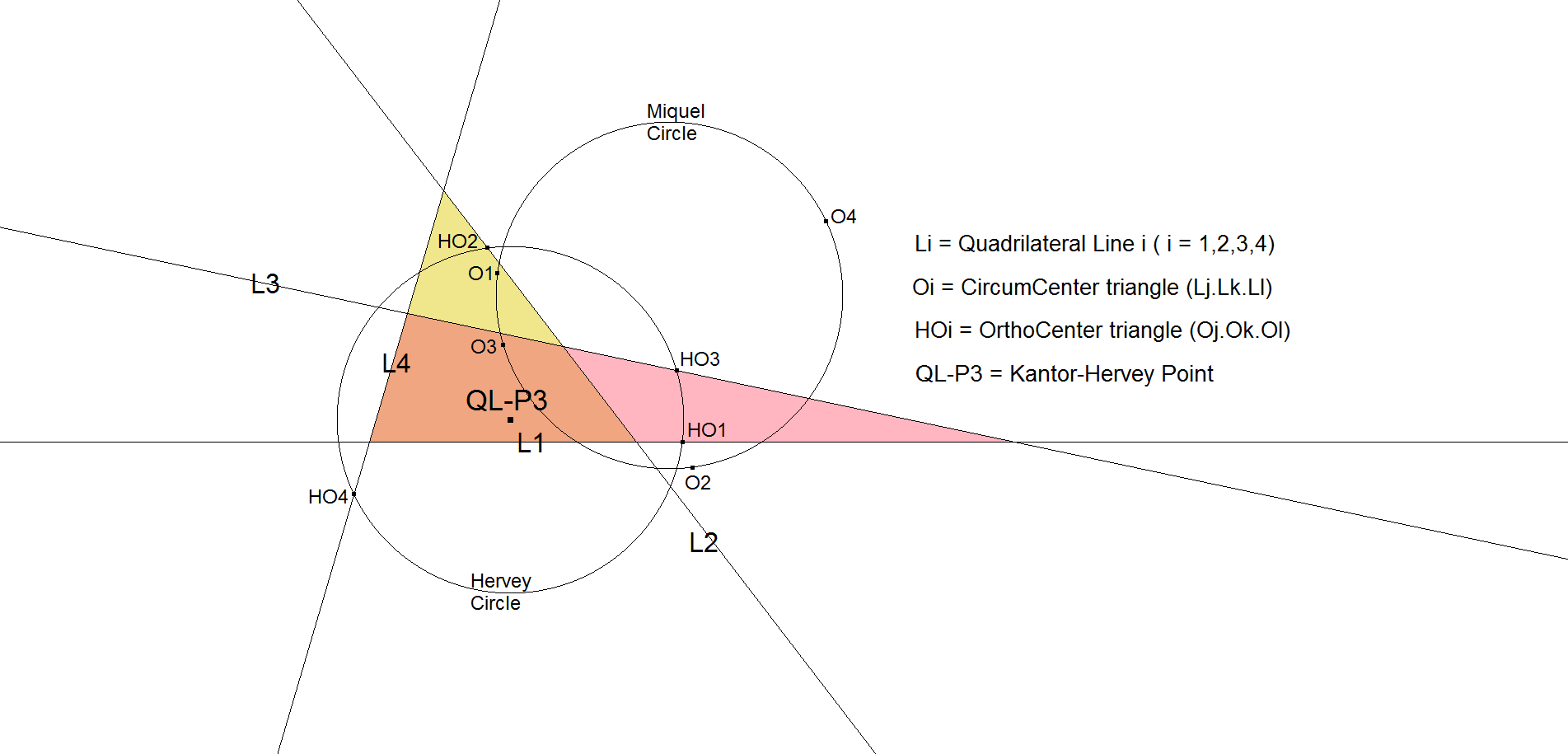
QL-P3: Kantor-Hervey Point

The circumcenters of the 4 component triangles of the Reference Quadrilateral are concyclic (on the Miquel Circle). These circumcenters Oi (i=1,2,3,4) form a Quadrangle with 4 component triangles whose Orthocenters HOi (i=1,2,3,4) are also concyclic (on the Hervey Circle) with circumcenter QL-P3, the Kantor-Hervey Point.

QL-P3 is also described by F. Morley (1902) as point p1, being the center of the inscribed deltoid of a 4-Line in [49] page 4.

There is a description of this point in [2b] Jean-Louis Ayme “ Le point de Kantor-Hervey”. Here the point is defined as the common point of the perpendicular bisectors of Oi.Hi (i=1,2,3,4), where Oi and Hi are resp. the Circumcenter and the Orthocenter of the Component Triangles of the Reference Quadrilateral.

There is also a description in [6] by Alain Levelut.

Infovisual QL-P3-infovisual-cvt-01.png
1st CT-coordinate

a2 (l – m) (l – n) (b2 n – c2 m) + (b2 – c2) (m – n) (-b2 (l – m) n + c2 m (l – n))

1st DT-coordinate

a4 – b4 (3 m2+n2)/(l2-n2) – c4 (m2+3 n2)/(l2-m2)

– 4 b2 c2 m2/(-l2+m2) – 4 b2 c2 n2/(-l2+n2) + 2 a2 (b2-c2) (m2+n2)/(m2-n2)

Properties
  • QL-P3 lies on this line:
  • Distances QL-P4.QL-P6 : QL-P6.QL-P5 : QL-P5.QL-P3 = 1 : 1 : 2.
  • QL-P2.QL-P3 = QL-L4 (Morley Line) // Newton Line QL-L1.
  • QL-P3 is also the point of concurrence of the four perpendicular bisectors of the segments Oi.Hi of the Euler Lines of the QL-Component Triangles Ti ([49], page 4 and [6] page 5).
  • QL-P3 is the center of the Hervey Circle (QL-Ci4).
  • QL-P3 is the center of the Kantor-Hervey Deltoid (QL-Qu2).
  • QL-P3 is the Gergonne-Steiner Point (QA-P3) as well as the Isogonal Center (QA-P4) as well as the Midray Homothetic Center (QA-P8) as well as the QA-DT-Orthocenter (QA-P12) from the Orthocenter Quadrangle in the Circumcenter Quadrangle H1.H2.H3.H4. These 4 QA-points concur. H1.H2.H3.H4 is concyclic.
  • d (QL-P3, QL-P2) = 3 * d (QL-P5 , QL-P12)
  • d (QL-P3, QL-L1) = d (OL-P2, QL-L1) = d (OL-P4, QL-L1), where d=distance and QL-L1=Newton Line.
  • QL-P3 is the endpoint of the vector being the sum of the vectors from QL-P4 to the 4 Circumcenters of the QL-Component Triangles. See [49].
  • The QL-P3-Triple Triangle in a Quadrangle is perspective with the QL-P2-Triple Triangle as well as the QL-P29-Triple Triangle with perspector QA-P15.


Estimated human page views: 650

Scroll naar boven