QA-Co4: QA-DT-P3-P12 Orthogonal Hyperbola
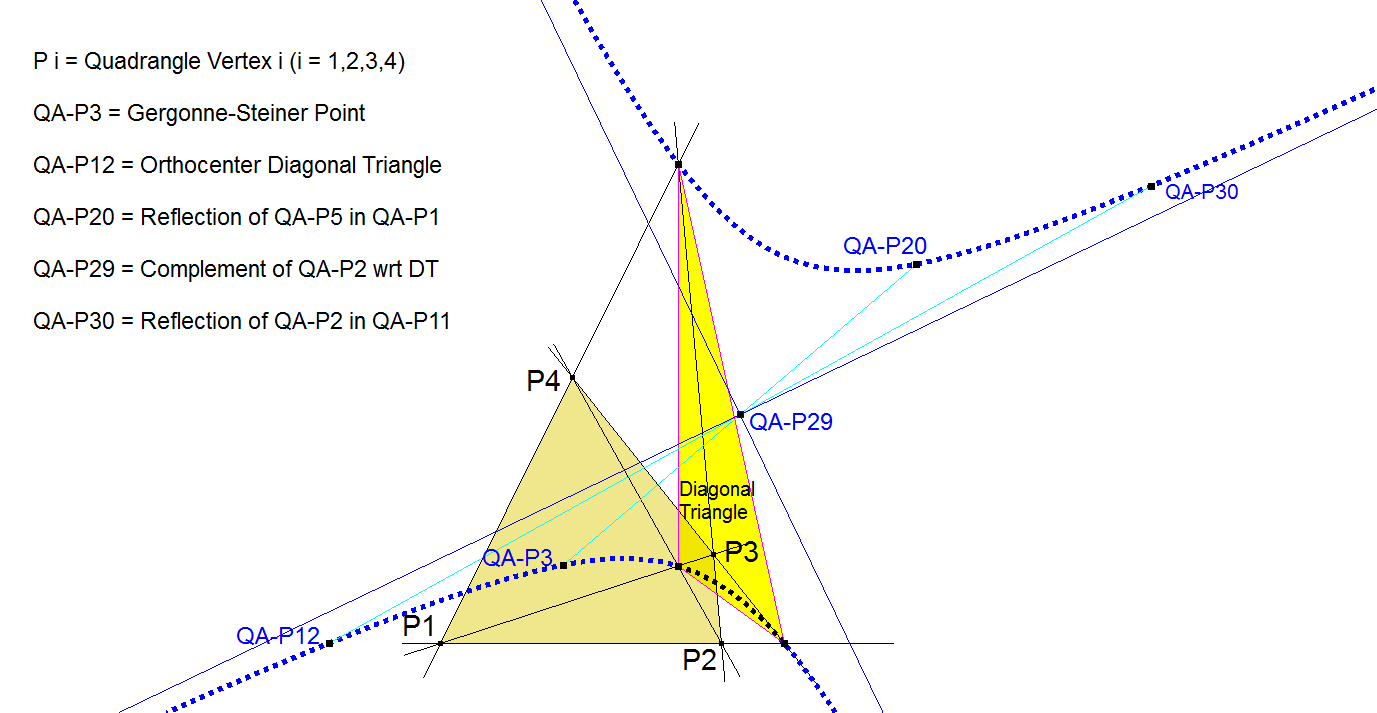
QA-Co4 is the circumscribed orthogonal hyperbola of the Diagonal Triangle (QA-DT) of the Reference Quadrangle passing through the Gergonne-Steiner Point (QA-P3).
Conic-equation in CT-notation:
(a2 (q – r) /(q + r) – b2 (p + 3 r)/(p + r) + c2 (p + 3 q)/(p + q)) q r x2
+ (a2 (q + 3 r) /(q + r) – b2 (p – r) /(p + r) – c2 (3 p + q) /(p + q)) p r y2
+ (-a2 (3 q + r)/(q + r) + b2 (3 p + r)/(p + r) + c2 (p – q) /(p + q)) p q z2
– (a2 (p q + q2 – p r + 3 q r)/(q + r) – b2 (p2 + p q + 3 p r – q r)/(p + r) + c2 (p – q)) r x y
– (a2 (p q – p r – 3 q r – r2) /(q + r) – b2 (p – r) + c2 (p2 + 3 p q + p r – q r)/(p + q)) q x z
– (a2 (q – r) – b2 (p q – 3 p r – q r – r2)/(p + r) – c2 (3 p q + q2 – p r + q r)/(p + q)) p y z = 0
Conic-equation in DT-notation:
((a2-b2) r2 – c2 (p2-q2)) x y
+ ((c2-a2) q2 – b2 (r2-p2)) x z
+ ((b2-c2) p2 – a2 (q2-r2)) y z = 0
1st CT-coordinate QA-DT-Conic Perspector (see QA-Co-1):
(a2 (p + q) (q – r) (p + r) (2 p + q + r) – b2 (p + q) (q + r) (2 p2 + p q + 3 p r – q r – r2) + c2 (p + r) (q + r) (2 p2 + 3 p q – q2 + p r – q r)) /
(a2 (p + q) (q – r) (p + r) – b2 (p + q) (q + r) (p + 3 r) + c2 (p + 3 q) (p + r) (q + r))
1st DT-Coordinate QA-DT-Conic Perspector (see QA-Co-1):
(b2 p2 – c2 p2 – a2 q2 + a2 r2)
(c4 p2 (p – q) q2 (p + q) (p2 – q2 – r2) + b4 p2 (p – r) r2 (p + r) (p2 – q2 – r2) + 2 b2 c2 p2 q2 r2 (3 p2 – q2 – r2) + a4 q2 r2 (p2 q2 – q4 + p2 r2 + 2 q2 r2 – r4) + a2 (-2 c2 p2 q2 r2 (p2 + q2 – r2) – 2 b2 p2 q2 r2 (p2 – q2 + r2)))
Properties
- QA-Co4 passes apart from the vertices of the Diagonal Triangle also through
- These intersection points also lie on conic QA-Co4:
- The center of QA-Co4 is QA-P29 (Complement of QA-P2 wrt the DT).
- QA-Co4 is the Involutary Conjugate (see QA-Tf2) of QA-L4 (Line through QA-P1, QA-P6 and QA-P23).
- The QA-DT-Conic Perspector (see QA-Co-1) of QA-Co4 is a point on the line QA-P22.QA-P29.
- The infinity points of the asymptotes of QA-Co4 are the QA-Tf2-images of the intersection points of QA-L4 and QA-Co1. See [34], QFG#2196.
- QA-Co4 is the QA-DT-isogonal conjugate of a line through QA-P11 parallel to QA-P4.QA-P12DT-isogonal conjugate of a line through QA-P11 parallel QA-P4.QA-P12,. See [34], QFG#2196.
Estimated human page views: 869
