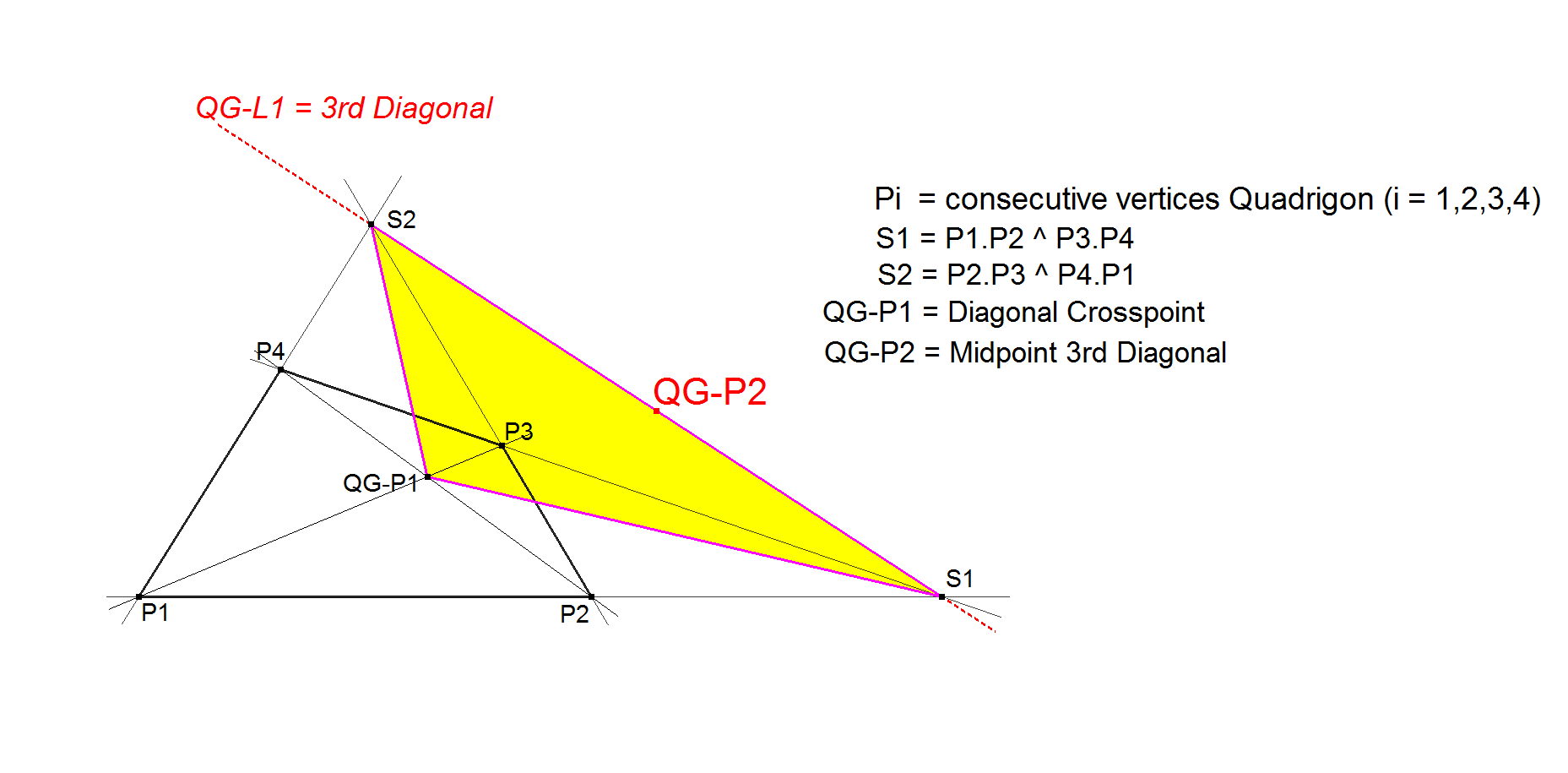
QG-P2 Midpoint 3^rd QA-Diagonal

We use this terminology:

• A “QA-Quadrigon” is a Quadrigon seen as the Component of a Quadrangle.
• A “QL-Quadrigon” is a Quadrigon seen as the Component of a Quadrilateral.

The 3^rd Diagonal of a QA-Quadrigon is the same line as the 3^rd Diagonal of a QL-Quadrigon. However the Midpoint of a QA-Quadrigon is different from the Midpoint of a QL-Quadrigon.

QG-P2 is the Midpoint of the segment on the 3^rd Diagonal of a QA-Quadrigon limited by the intersection points with the 3^rd Diagonals of the 2 other Component QA-Quadrigons.

Construction

Let S1 = P1.P2 ^ P3.P4 and S2 = P2.P3 ^ P4.P1.

QG-P2 = the Midpoint of S1 and S2.

CT-Coordinates QG-P2 in 3 QA-Quadrigons:

(p (2 p + q + r) : q (p + r) : r (p + q))

(p (q + r) : q (p + 2 q + r) : r (p + q))

(p (q + r) : q (p + r) : r (p + q + 2 r))

CT-Coordinates QG-P2 in 3 QL-Quadrigons:

(m – n : -n : m)

(n : n – l : -l)

(-m : l : l – m)

CT-Area of QG-P2-Triangle in the QA-environment:(equals ¼ x area QL-Diagonal Triangle)

p q r Δ /(2 (p + q) (p + r) (q + r))

CT-Area of QG-P2-Triangle in the QL-environment:(points are collinear)

0

—

DT-Coordinates QG-P2 in 3 QA-Quadrigons:

(1 : 0 : 1)

(0 : 1 : 1)

(1 : 1 : 0)

DT-Coordinates QG-P2 in 3 QL-Quadrigons:

(n² : 0 : – l² )

(0 : n² : -m²)

(m² : – l² : 0)

DT-Area of QG-P2-Triangle in the QA-environment:(equals ¼ area QA-Diagonal Triangle)

S / 8

DT-Area of QG-P2-Triangle in the QL-environment:(points are collinear)

0

Properties

• QG-P2 lies on these lines:
  • QG-P1.QA-P10
  • QG-P13.QG.P14
  • QA-P1.QG-P12                         = Newton Line
  • QA-P5.QG-P4
  • QA-P20.QG-P15             (1 : 1 = Midpoint of QA-P20 and QG-P15)
  • QG-2P2a/b.QG-2P3a/b           = QG-L1 = 3^rd Diagonal of the Quadrigon
• QG-P2 is the fourth harmonic point of QG-P12 (Inscribed Harmonic Conic Center) on the Newton Line (QL-L1) wrt the midpoints of the diagonals (note Eckart Schmidt).
• The triangle formed by the 3 QA-Versions of QG-P2 is the medial triangle of the QA-Diagonal Triangle.
• The 3 QL-Versions of QG-P2 are 3 points on the Newton Line QL-L1 with centroid QL-P12. See [66], QPG-message#1271.
• The Polar (see [13], Polar) of QG-P2 wrt QG-Co1 as well as QG-Co2 is the line QG-P1.QG-P3.
• The circle defined by the 3 versions of QG-P2 (QA-Ci2) in a Quadrangle is incident with QA-P17, QA-P29, QA-P36 and the foci of the QA-parabolas (QA-2Co1).
• The Triple Triangle of QG-P2 is perspective with all QA-Component Triangles (see QA-Tr-1 for Desmic Triple Triangles).

Estimated human page views: 532