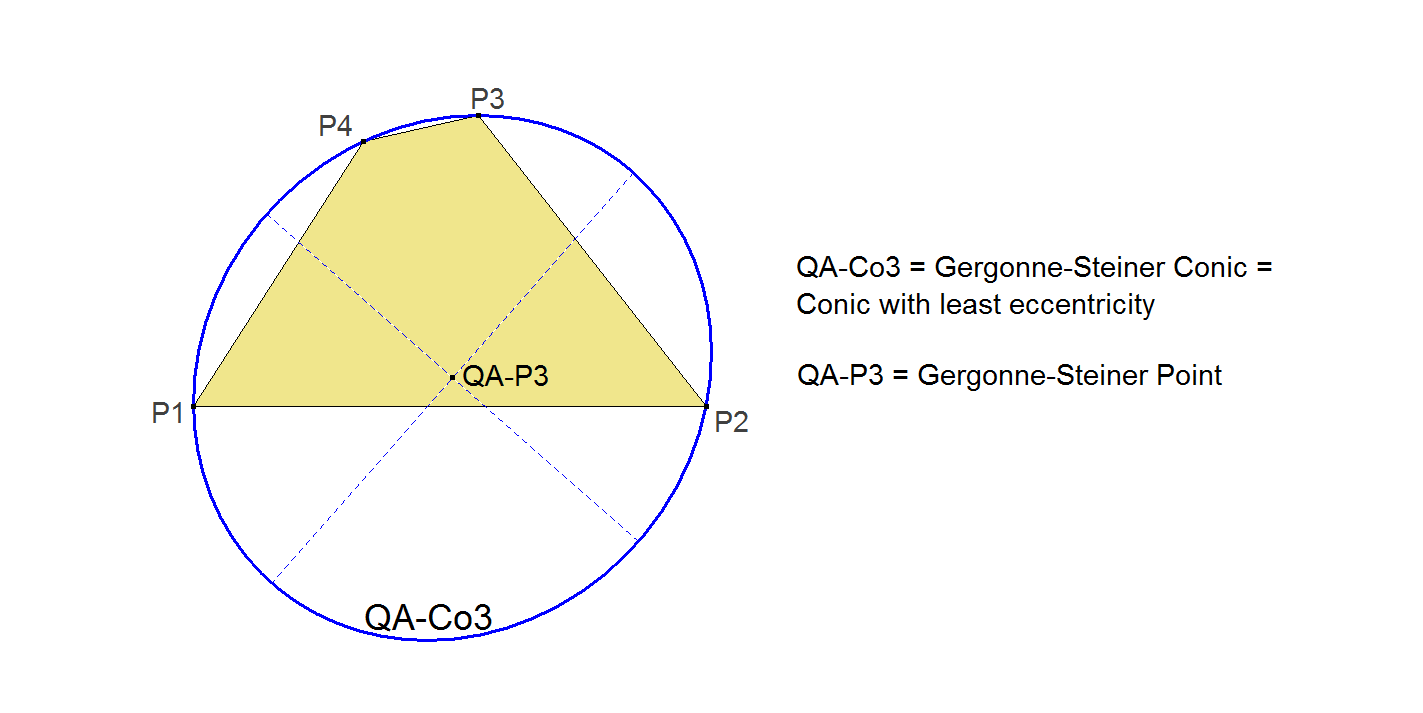
QA-Co3: Gergonne-Steiner Conic
In a random quadrangle it is generally impossible to circumscribe a circle through all 4 points. But it is always possible to circumscribe a conic (ellipse, parabola or hyperbola) through these 4 points. Technically, the conic with least eccentricity is the conic that deviates least from a circle.
The Gergonne-Steiner Conic is the conic through the vertices of the Reference Quadrangle with least eccentricity. It is the conic with center QA-P3 (Gergonne-Steiner Point). The problem of the Quadrangle conic with least eccentricity was initially posed in the “Annales de Gergonne” and solved by J. Steiner. See [7] page 231.
Equation CT-notation:
(a2 p q r (2p+q+r) – (b2 r +c2 q) p2 (q+r)) y z
+ (b2 p q r (p+2q+r) – (c2 p +a2 r) q2 (p+r)) z x
+ (c2 p q r (p+q+2r) – (a2 q+b2 p) r2 (p+q)) x y = 0
Equation DT-notation:
(2 a2 q2 r2 – b2 r2 (p2+q2-r2) – c2 q2 ( p2 – q2+r2)) x2
+(2 b2 p2 r2 – a2 r2 (p2+q2-r2) – c2 p2 (-p2+q2+r2)) y2
+(2 c2 p2 q2 – a2 q2 (p2-q2+r2) – b2 p2 (-p2+q2+r2)) z2 = 0
Properties
- Jean-Pierre Ehrmann commented on this conic that when e = eccentricity,
- then for this conic e2 = √ [2/(k+1)],
- where k = O1P1*/R1 = O2P2*/R2 = O3P3*/R3 = O4P4*/R4,
- Oi = circumcenter PjPkPl,
- Pi*= isogonal conjugate of Pi wrt PjPkPl,
- Ri = circumradius PjPkPl.
- (See Hyacinthos [11] message #19970)
- Let d1=QA-P3.QA-P2 and d2=QA-P3.QA-P4. Now d1/d2 = (a2 – b2)/(a2 + b2) when QA-Co3 is an ellipse and d1/d2=(a2 – b2)/(a2 + b2) when QA-Co3 is a hyperbola, where a and b are resp. the major and minor axes of QA-Co3 (Benedetto Scimemi, November 12, 2014).
- The axes of the Gergonne-Steiner Conic can be constructed as the angle bisectors of the angle QA-P2.QA-P3.QA-P4 (Benedetto Scimemi, November 12, 2014).
- The axes of the Gergonne-Steiner Conic are parallel to:
- The QA-Diagonal Triangle (QA-Tr1) is self-polar wrt QA-Co3.
Estimated human page views: 794
