QA-Cu2: QA-DT-P5 Cubic
QA-Cu2 is the locus of the Doublepoints created by the QA-Line Involution (QA-Tf1) of all lines through QA-P5. It is a pivotal isocubic of the Diagonal Triangle, invariant wrt the Involutary Conjugate wrt pivot QA-P5.
QA-Cu2 is a pK(QA-P16,QA-P5) cubic wrt the QA-Diagonal Triangle in the terminology of Bernard Gibert (see [17b]). (note Eckart Schmidt)
Equation CT-notation:
(p+q) (p+q+2r) (q x – p y) x y
+ (p+r) (p+2q+r) (p z – r x) x z
+ (q+r) (2p+q+r) (r y – q z) y z = 0
Equation DT-notation:
(4 (p4+q2 r2) – (p2+q2+r2)2) (r2 y2-q2 z2) x
+ (4 (q4+p2 r2) – (p2+q2+r2)2) (p2 z2-r2 x2) y
+ (4 (r4+p2 q2) – (p2+q2+r2)2) (q2 x2-p2 y2) z = 0
Properties
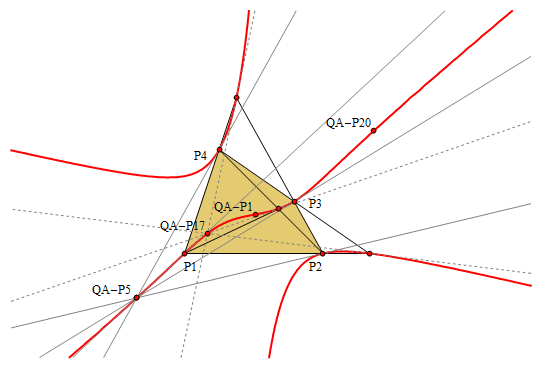
- These points lie on QA-Cu2:
- the vertices of the Reference Quadrangle
- the vertices of the QA-Diagonal Triangle
- the Involutary Conjugate pair (QA-P1, QA-P20)
- the Involutary Conjugate pair (QA-P5, QA-P17)
- the 3 versions of QG-P15 and their Involutary Conjugate QG-P1.QA-P20 ^ QG-P2.QG-P12 ^ QG-P8.QA-P10 ^ QG-P14.QA-P5, which is the Infinity point of the Newton Line in corresponding QA-Quadrigon, representing one of the asymptotes.
- the intersection point QA-P1.QA-P17 ^ QA-P16.QA-P20, which is also the perspector of the QG-P12 Triple Triangle and the QG-P15 Triple Triangle. See also QA-Tr-2.
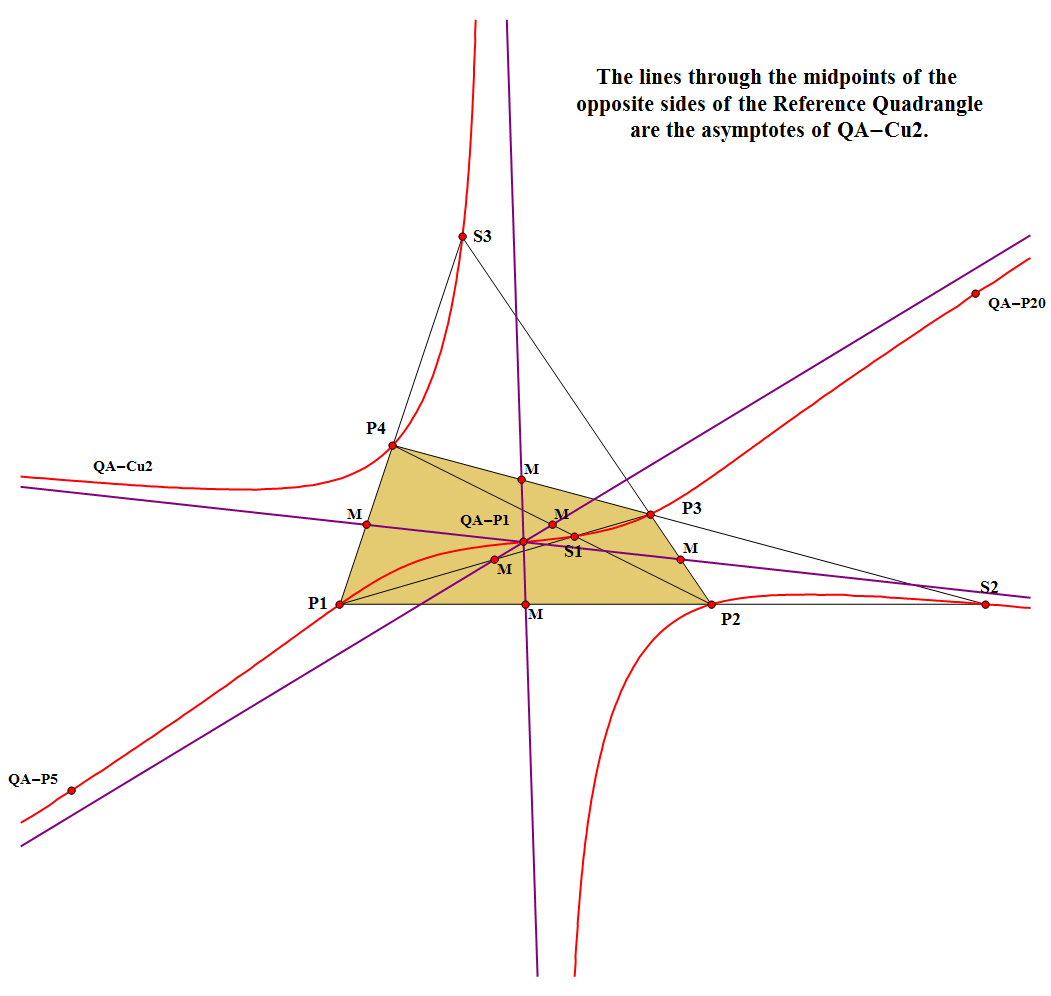
- The lines M12.M34, M13.M24, M14.M23 are the asymptotes of QA-Cu2, where Mij is the Midpoint of Pi.Pj and (i,j) ∈ (1,2,3,4).
- The 3 asymptotes of QA-Cu2 meet at QA-P1.
- The tangents at P1, P2, P3, P4 meet at QA-P5.
- The tangents at S1, S2, S3 and QA-P5 meet at QA-P17 which is the Involutary Conjugate of QA-P5 on the cubic.
- The QA-Cu2 cubic is symmetrical wrt QA-P1 (note Eckart Schmidt).
Estimated human page views: 658
