QA-Tf9: QA-5th Point Tangent
QA-Tf9 maps a point P to the tangent at P to the circumscribed conic of P1,P2,P3,P4,P. It is the dual of QL-Tf7.
Construction
Definition of Triangle Transformation TR-Tfx:
TR-Tfx(ABC,P,Pi) = P-Isoconjugate wrt triangle ABC of P.
It can be constructed as QA-Tf2(Pi) wrt quadrangle (Pa,Pb,Pc,P) , where Pa,Pb,Pc are the vertices of the Anticevian Triangle of P wrt ABC (construction of Eckart Schmidt, see [34], QFG#2145, #2148).
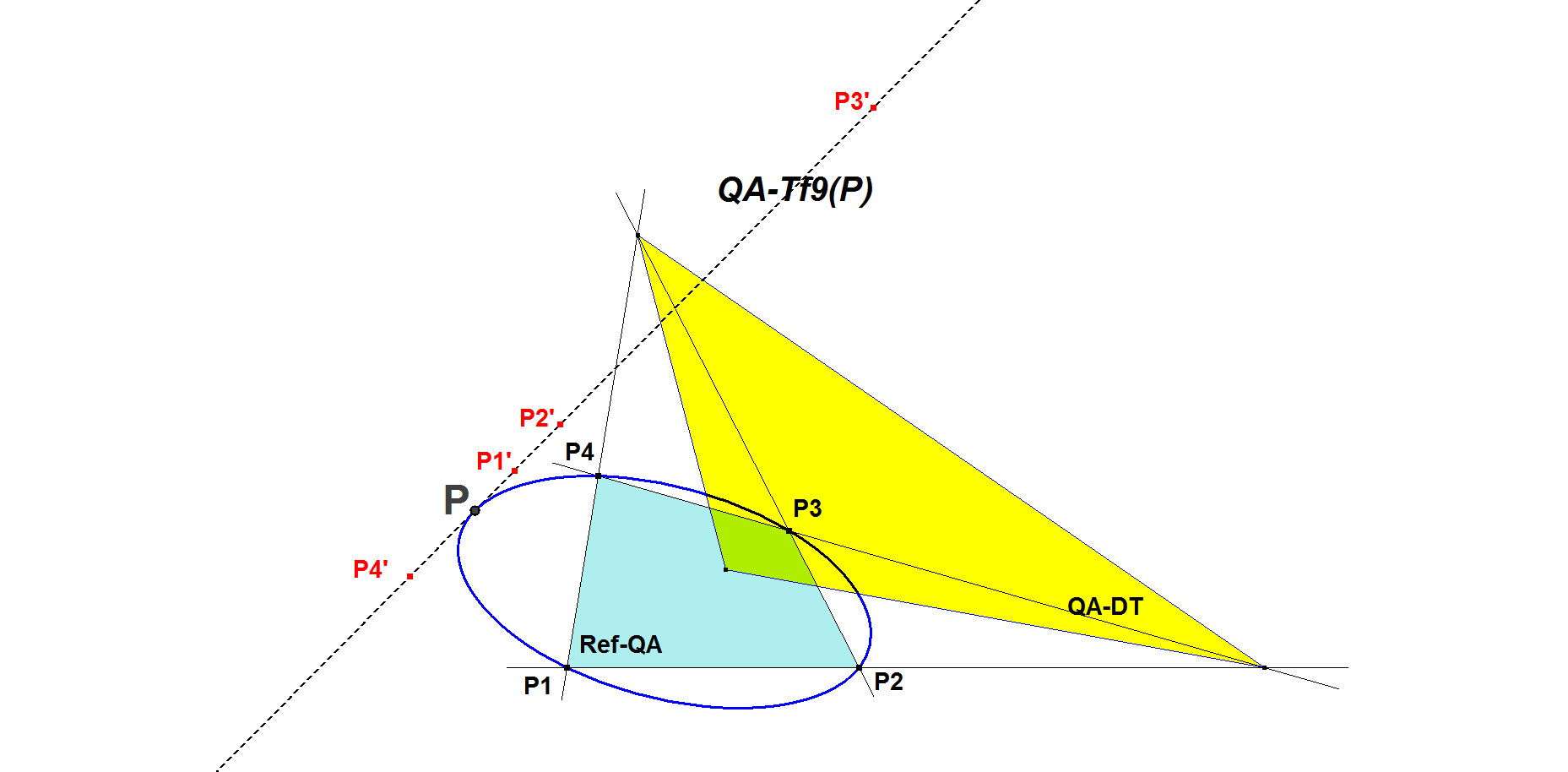
Let P1, P2, P3, P4 be the basic points of the Reference Quadrangle, also referred to as Pi (i=1,2,3,4). Let P be some random point. Let QA-DT = Diagonal Triangle QA-Tr1.
Then QA-Tf9(P) is the line on which P and the 4 occurrences of Pi’ = TR-Tfx(QA-DT,P,Pi) are collinear.
Construction of 5th Point Tangent at an infinity point:
The 5th Point Tangent at an infinity point is actually the infinity point of the asymptote of a circumscribed QA-Hyperbola.
Let P0 be the Infinity Point of some line named L0.
Let L1 and L2 be two random lines.
Then 5th-point-tangent QA-Tf9(P0) can be drawn by constructing QA-Tf18(L1,L0) and QA-Tf18(L2,L0) and by connecting both obtained QA-Tf14-points. See [34], QFG#3713.
The envelope of all 5th-point-tangents at an infinity point is a quartic touching all six sides of the Quadrangle. It is the same quartic as mentioned by Eckart Schmidt in [34], QFG#141.
CT-Coordinates
Let P (x : y : z) be the 5th point, then QA-Tf9(P) is
(p y z (r y – q z) : q x z (-r x + p z) : r x y (q x – p y))
Properties
- QA-Tf9(QA-Px) is the line through QA-Px, QA-Tf2(QA-Px), QA-Tf5(QA-Px).
- When QA-Px and QA-Py are involutary conjgates (QA-Tf2), then QA-Tf9(QA-Px)=QA-Tf9(QA-Py)=QA-Px.QA-Py.
- The Crosspoint(P,Pi) wrt triangle Pj.Pk.Pl (i,j,k,l are different numbers from (1,2,3,4)) lies on the 5th point tangent of P. See [13], keyword Crosspoint.
Table of 5th Point Tangents
| QA-point | QA-Tf9 [QA-point] |
|---|---|
| QA-P1 | QA-P1.QA-P5.QA-P10.QA-P20.QA-P22.QA-P25.QA-P43 (= QA-L3) |
| QA-P2 | QA-P2.QA-Pxx |
| QA-Pxx = QA-P2.QA-Tf2(QA-P2) ^ QA-P4.QA-Tf2(QA-P4) = point on QA-Cu7 | |
| QA-P3 | QA-P3.QA-P4 |
| QA-P4 | QA-P4.QA-P41.QA-Tf4(QA-P2).QA-Tf4(QA-P6).QA-Pxx |
| QA-Pxx = QA-P2.QA-Tf2(QA-P2) ^ QA-P4.QA-Tf2(QA-P4) = point on QA-Cu7 | |
| QA-P5 | QA-P5.QA-P17.QA-P19.QA-P21 |
| QA-P6 | QA-P6.QA-P30 |
| QA-P10 | QA-P10.QA-P16.QA-P19.QA-P31 |
| QA-P11 | QA-P11.QA-P18.QA-P19 |
| QA-P12 | QA-P12.QA-P23 |
| QA-P16 | QA-P10.QA-P16.QA-P19.QA-P31 |
| QA-P17 | QA-P5.QA-P17.QA-P19.QA-P21 |
| QA-P18 | QA-P18.QA-P19 |
| QA-P20 | QA-P1.QA-P5.QA-P10.QA-P20.QA-P22.QA-P25.QA-P43 (= QA-L3) |
| QA-P21 | QA-P21.QA-P27 |
| QA-P23 | QA-P12.QA-P23 |
| QA-P27 | QA-P21.QA-P27 |
| QA-P30 | QA-P6.QA-P30 |
| QA-P41 | QA-P4.QA-P41.QA-Tf4(QA-P2).QA-Tf4(QA-P6).QA-Pxx |
| QA-Pxx = QA-P2.QA-Tf2(QA-P2) ^ QA-P4.QA-Tf2(QA-P4) = point on QA-Cu7 |
Estimated human page views: 562
