← Previous Next →

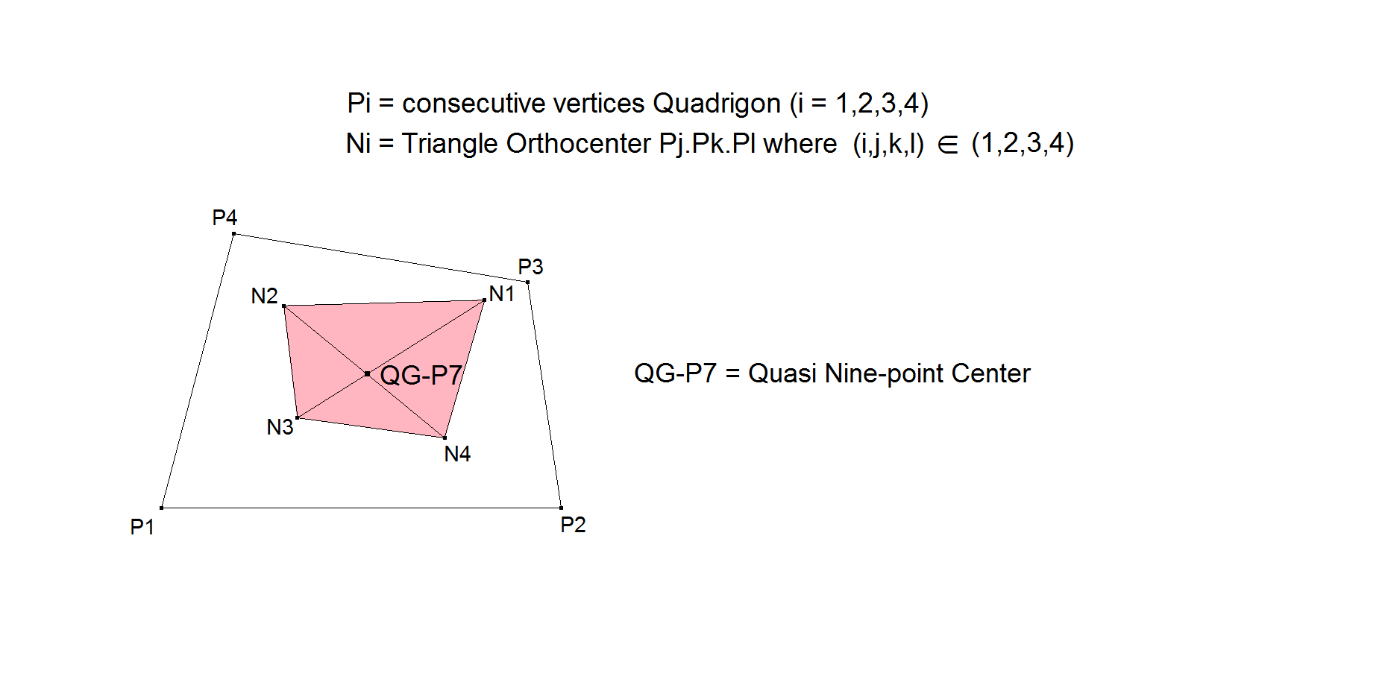
QG-P7: 1st Quasi Nine-point Center

The 1st Quasi Circumcenter is the Diagonal Crosspoint of the X5-Quadrigon.

The X5-Quadrigon is defined by its vertices being the Triangle Nine-point Centers of the component triangles of the Reference Quadrigon.

This point and other 1st Quasi points are described in [5].

Infovisual QG-P7-infovisual-cvt-01.png
CT-Coordinates QG-P7 in 3 QA-Quadrigons (only coordinates of 1st Quadrigon point are given)

(a4 q (p + r) – c4 (p + r) (p + q + r) + b4 (-p2 – p r – q r – r2) + b2 c2 (2 p2 + p q + 3 p r + 2 q r + 2 r2) + a2 (c2 (p + r)2 + b2 (p2 – p q + 3 p r + 2 q r + r2)) :

-a4 (p + r) (p + 2 q + r) – c4 (p + r) (p + 2 q + r) + b4 (-p q – 2 p r – q r) + b2 c2 (p2 + p q + 2 p r + 3 q r + r2) + a2 (2 c2 (p + r) (p + 2 q + r) + b2 (p2 + 3 p q + 2 p r + q r + r2)) :

c4 q (p + r) – a4 (p + r) (p + q + r) + b4 (-p2 – p q – p r – r2) + b2 c2 (p2 + 2 p q + 3 p r – q r + r2) + a2 (c2 (p + r)2 + b2 (2 p2 + 2 p q + 3 p r + q r + 2 r2)))

CT-Coordinates QG-P7 in 3 QL-Quadrigons (only coordinates of 1st Quadrigon point are given)

((-a4 – b4 + 2 a2 c2 + 2 b2 c2 – c4) m3 n + (-a2 b2 + b4 – a2 c2 – 2 b2 c2 + c4) m2 n2 + l2 ((-a2 b2 + b4 – a2 c2 – 2 b2 c2 + c4) m2 – 2 (a4 – a2 b2 + b4 – a2 c2 – 2 b2 c2 + c4) m n + (-a2 b2 + b4 – a2 c2 – 2 b2 c2 + c4) n2) + l ((-a4 + 3 a2 b2 – 2 b4 + 2 a2 c2 + 3 b2 c2 – c4) m3 + 2 (2 a4 – 2 a2 b2 + 2 b4 – 3 a2 c2 – 3 b2 c2 + c4) m2 n + (2 a2 b2 – 2 b4 + 3 a2 c2 + 3 b2 c2 – c4) m n2) :

b2 (a2 + b2 – c2) m3 n + (a4 – a2 b2 – 2 a2 c2 – b2 c2 + c4) m2 n2 + l2 ((a4 – a2 b2 – 2 a2 c2 – b2 c2 + c4) m2 + (-a4 + 3 a2 b2 + 3 a2 c2 + 2 b2 c2 – 2 c4) m n + (a4 – a2 b2 – 2 a2 c2 – b2 c2 + c4) n2) + l (-b2 (a2 – b2 – c2) m3 – 2 b2 (a2 + b2 + c2) m2 n + (-2 a4 + 2 a2 b2 + 3 a2 c2 + 3 b2 c2 – c4) m n2) :

(-a4 + 3 a2 b2 – 2 b4 + 2 a2 c2 + 3 b2 c2 – c4) m3 n + (a4 – 2 a2 b2 + b4 – a2 c2 – b2 c2) m2 n2 + l2 ((a4 – 2 a2 b2 + b4 – a2 c2 – b2 c2) m2 + (-a4 + 3 a2 b2 – 2 b4 + 3 a2 c2 + 2 b2 c2) m n + (a4 – 2 a2 b2 + b4 – a2 c2 – b2 c2) n2) + l ((-a4 + 2 a2 b2 – b4 + 2 a2 c2 – c4) m3 + 2 (a4 – 3 a2 b2 + 2 b4 – 3 a2 c2 – 2 b2 c2 + 2 c4) m2 n – 2 (a4 – 2 a2 b2 + b4 – a2 c2 – b2 c2 + c4) m n2))

CT-Area of QG-P7-Triangle in the QA-environment

(a4 q r (p + q) (p + r) + b4 p r (p + q) (q + r) + c4 p q (p + r) (q + r) – 2 b2 c2 p q r (q + r) – 2 a2 c2 p q r (p + r) – 2 a2 b2 p q r (p + q))

/ (32 Δ (p + q) (p + r) (q + r) (p + q + r))

CT-Area of QG-P7-Triangle in the QL-environment

T1 T2 /(64 Δ (l – m)2 (l – n)2 (m – n)2 (-l m + l n + m n) (l m + l n – m n) (l m – l n + m n))

where: T1 = a2 m n (l – m) (l – n) + b2 l n (m – l) (m – n) + c2 l m (n – l) (n – m)

T2 = a2 m n (l – m) (l – n) (-3 l m + l n + m n) (l m – 3 l n + m n)

+ b2 l n (m – l) (m – n) (l m + l n – 3 m n) (-3 l m + l n + m n)

+ c2 l m (n – l) (n – m) (l m + l n – 3 m n) (l m – 3 l n + m n)

–

DT-Coordinates QG-P7 in 3 QA-Quadrigons (only coordinates of 1st Quadrigon point are given)

((-p2+q2+r2)(Sc a2 r2+Sb Sa p2-3 S2 p2)+2 Sb q2 (a2 r2-c2 p2) :

-(S2+Sa2) p2 (p2+q2-r2)-( S2+Sc2) r2 (-p2+q2+r2)+2 q2 (-Sa Sb p2+S2 q2-Sb Sc r2) :

(p2+q2-r2) (-3 S2 r2+Sa c2 p2+Sb Sc r2)+2 Sb q2 (c2 p2-a2 r2))

DT-Coordinates QG-P7 in 3 QL-Quadrigons (only coordinates of 1st Quadrigon point are given)

(-m2 (-Sb a2 l2+(S2+ Sb Sc) m2-(S2-Sb2) n2) : Sa a2 l2 m2+Sb b2 m4+c2 Sc m2 n2-2 S2 l2 n2 : -m2 (-(S2-Sb2) l2+( Sa Sb+S2) m2-Sb c2 n2))

CT-Area of QG-P7-Triangle in the QA-environment

-(a2 b2 r4+b2 c2 p4+a2 c2 q4-2 Sa a2 q2 r2-2 Sb b2 p2 r2-2 c2 Sc p2 q2) / (8 S (-p+q+r) (p+q-r) (p-q+r) (p+q+r))

CT-Area of QG-P7-Triangle in the QL-environment

(Sc (l2-m2)2+Sb (l2-n2)2+Sa (m2-n2)2) (Sc n4 (l2-m2)2 +Sb m4 (l2-n2)2+Sa l4 (m2-n2)2) / (8 S (l2-m2)2 (l2-n2)2 (m2-n2)2)

Properties
  • QG-P4, QG-P5, QG-P6, QG-P7 are collinear on QG-L4, the 1st QG-Quasi Euler Line.
  • QG-P7 is the Midpoint of QG-P10 and QG-P15.
  • QG-P7 is the Reflection of QG-P1 in QG-P11.
  • QG-P7 is the Reflection of QG-P9 in the line QG-P2.QG-P12 (which coincides with the Newton Line QL-L1).
  • QG-P7 is the Nine-point center of the 1st QG-Quasi Diagonal Triangle: QG-Tr1.
  • QA-P1 (QA-Centroid) lies on the circumcircle of the triangle formed by the 3 QA-versions of QG-P7.
  • QL-P2 (Morley Point) lies on the circumcircle of the triangle formed by the 3 QL-versions of QG-P7.
  • The area of the QA-versions of QG-P7 = the area of the QA-versions of QG-P9.
  • The area of the QL-versions of QG-P7 = the area of the QL-versions of QG-P9.
  • QA-P15 is the Orthocenter of the Triangle formed by the 3 QA-versions of QG-P7 (note Eckart Schmidt).
  • The QA-Orthopole (QA-Tf3) of QG-P5 is QG-P7.


Estimated human page views: 506

Scroll naar boven