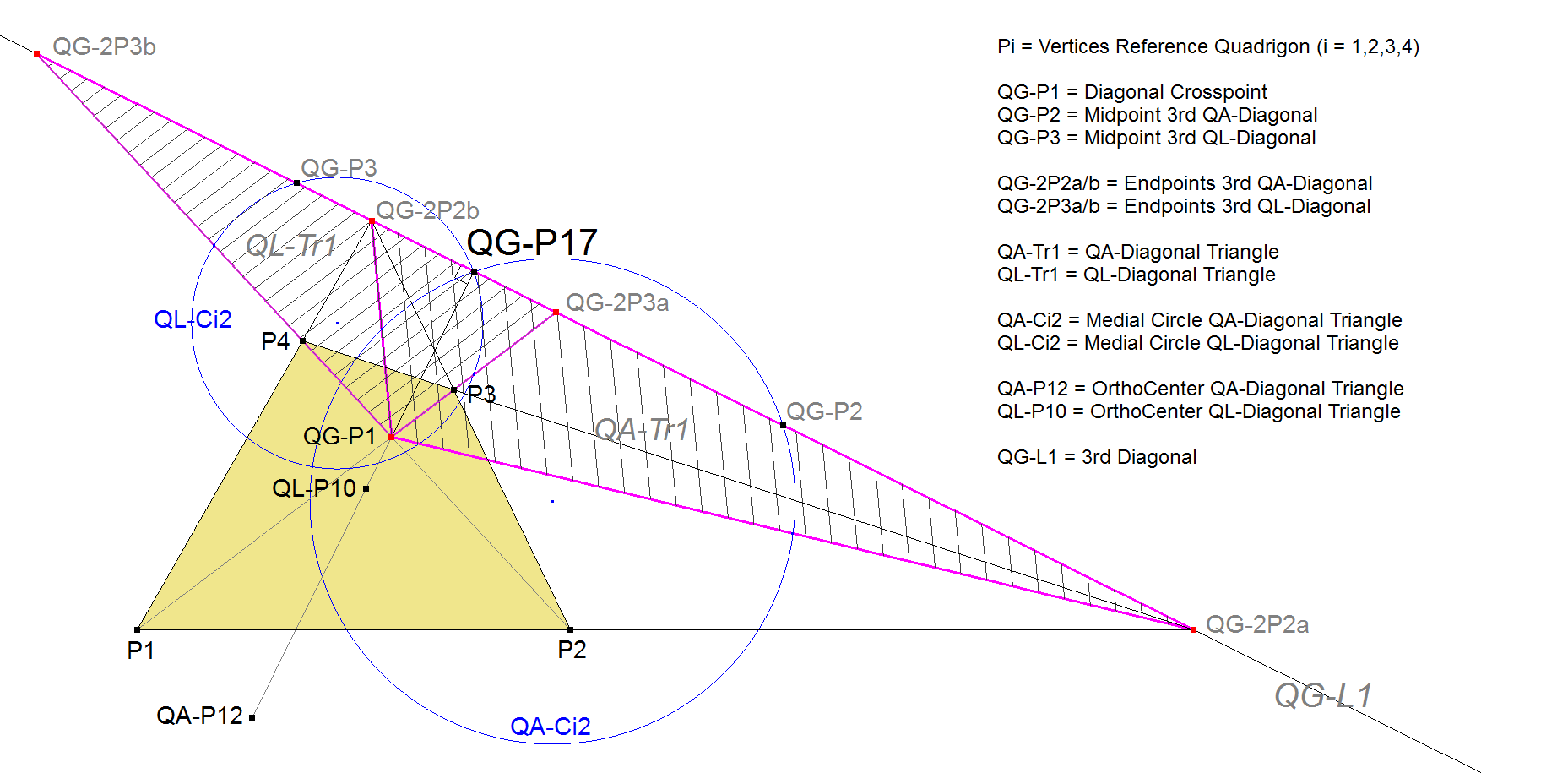
QG-P17: Projection Point of QG-P1 on QG-L1

QG-P17 is the projection of QG-P1 on QG-L1.

This point and its properties were found by Eckart Schmidt (October 5, 2012).

CT-Coordinates in 1^st QA-Quadrigon

(-p (c² p² q (q + r) + r (b² p² (q + r) – a² q (p² + q r))) :

p q r (a² q (p – r) + c² q (-p + r) – b² (p q + 2 p r + q r)) :

(-p – q) (b² p + a² q) r³ + c² p q r (p q + r²))

DT-Coordinates in 1^st QA-Quadrigon

(SC : 0 : SA)

CT-Coordinates in 1^st QL-Quadrigon

(m n (a² l² – c² n²) :

l n (a² (l – m) (l – n) + c² (l – n) (m – n) – b² (l m – l n + m n)) :

-l m(a² l² – c² n²))

DT-Coordinates in 1^st QL-Quadrigon

(SC : 0 : SA)

Properties

• QG-P17 lies on these lines:
  • QG-P1.QL-P10.QA-P12
  • QG-P2.QG-P3 (=QG-L1)
• QG-P17 lies on the medial circles QA-Ci2 and QL-Ci2.
• The 3 QL-versions of QG-P17 are the vertices of the Orthic Triangle of the QL-Diagonal Triangle (QL-Tr1) and lie on QA-Cu7.
• QG-P17 is the second focus of an inscribed conic with its first focus in QG-P18.
• QG-P17 is the QL-Tf1 image of QG-P18.
• The Polar (see [13], Polar) of QG-P17 wrt any inscribed or circumscribed conic of the Reference Quadrigon is a line through QG-P1.
• The QA-Orthopole (QA-Tf3) of QG-P17 is the Midpoint (QG-P1.QG-P18).
• QG-P17.QG-P1 is the Angle Bisector of angles P1.QG-P17.P3 and P2.QG-P17.P4.
• The Triple Triangle of QG-P17 is perspective with all QA-Component Triangles (see QA-Tr-1 for Desmic Triple Triangles).

Estimated human page views: 452