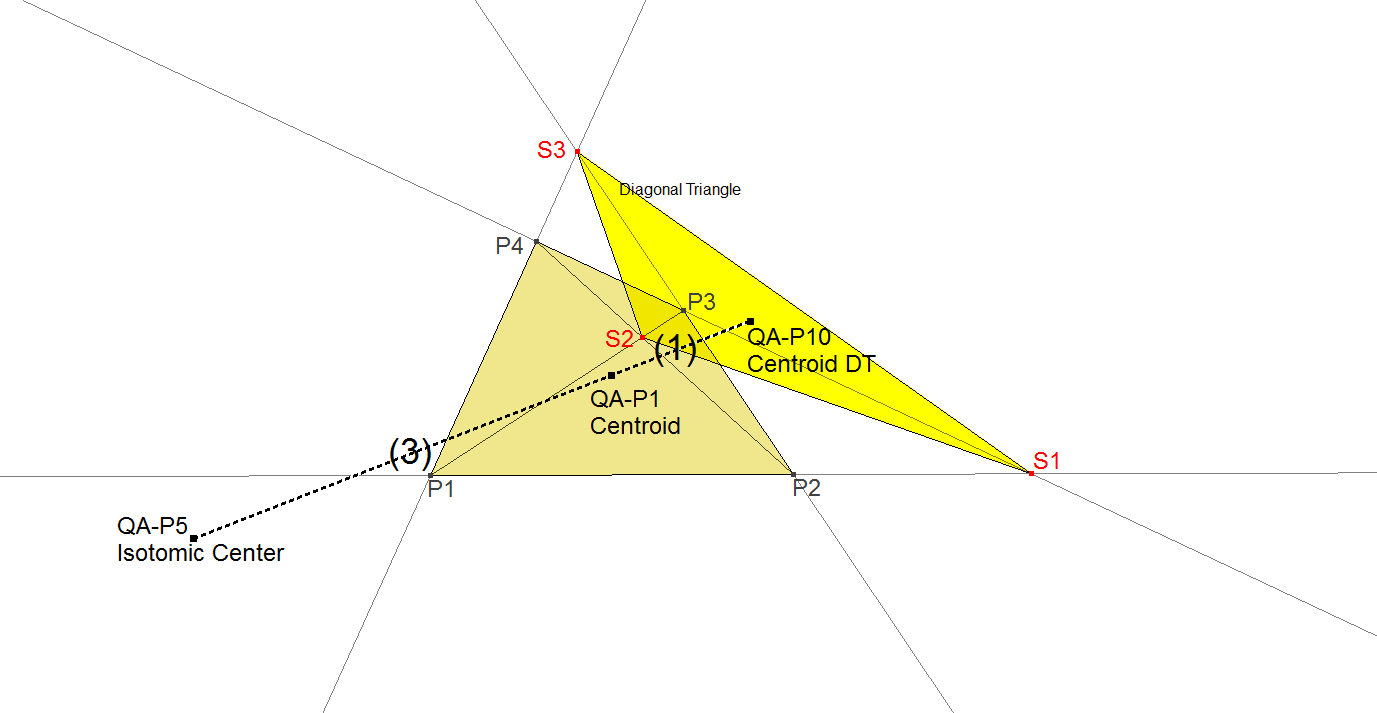
QA-P10: Centroid of the QA-Diagonal Triangle

QA-P10 is the Centroid of the Diagonal Triangle (QA-Tr1) of a Quadrangle.
The Diagonal Triangle of a Quadrangle P1.P2.P3.P4 is the triangle built from the intersection points S1 = P1.P2 ^ P3.P4, S2 = P1.P3 ^ P2.P4 and S3 = P1.P4 ^ P2.P3.
These points have CT-coordinates:  S1 = (p : q : 0),  S2 = (p : 0 : r),  S3 = (0 : q : r).
Because of the symmetry in S1, S2, S3 all Triangle Centers wrt S1.S2.S3 as described in [12] Clark Kimberling’s Encyclopedia of Triangle Centers also will be Quadrangle Centers. However only those points contributing to the points derived from component Quadrigons or component triangles will be described here as Quadrangle Centers.
The Centroid of the Diagonal Triangle does contribute to the points described earlier. The relation with the Isotomic Center QA-P5 is most special.

1st CT-Coordinate:

p (q + r) (2 p + q + r)

1st DT-Coordinate:

1

Properties:

• QA-P10 lies on these QA-lines:
  • QA-P1.QA-P5 (4 : -1)
  • QA-P2.QA-P29 (2 : 1 => QA-P29=Complement of QA-P2 wrt QA-DT)
  • QA-P4.QA-P28 (4 : -1)
  • QA-P11.QA-P12 (1 : 2 => QA-P11=Complement of QA-P19 wrt QA-DT)
  • QA-P16.QA-P19 (1 : 2 => QA-P16=Complement of QA-P19 wrt QA-DT)
  • QA-P30.QA-P36 (2 : 1 => QA-P36=Complement of QA-P30 wrt QA-DT)
• QA-P10 lies on these QG-line:
  • QG-P1.QG-P2 (2 : 1 => QG-P2=Complement of QA-P1 wrt QA-DT)
  • QG-P4.QL-P12 (2 : -1 => QA-P10 = Reflection of QG-P4 in QL-P12)
• QA-P10 is the Reflection of QA-P25 in QA-P26.
• QA-P5.QA-P1 : QA-P1.QA-P10 : QA-P10.QA-P20 = 3 : 1 : 2.
  This is the same ratio as used in the construction of the Quadrangle Centroid G using component triangles (when Gi = Centroid Pj.Pk.Pl then Pi.G : G.Gi = 3 : 1).
  As a consequence Quadrangle S1.S2.S3.QA-P5 and the Reference Quadrangle P1.P2.P3.P4 share the same Centroid (QA-P1).
• QA-P10 is the Involutary Conjugate (see QA-Tf2) of QA-P16.
• QA-P10 lies on the Conic through P1, P2, P3, P4 and QA-P5.
• QL-P15 is the Centroid of the QL-Triangle formed by the 3 QL-versions of QA-P10 (note Eckart Schmidt).
• QA-P10 is the Isotomic Center (QA-P5) of the Centroid Quadrangle (Eckart Schmidt, August 24, 2012).
• QA-P10 is the Perspector of the Triple Triangles (see QA-Tr-1) of these pairs {QG-P1, QG-P2}, {QG-P4, QL-P12}.
• QA-P2 is the Parallellologic Center of the QL-P8 Triple Triangle wrt the Triple Triangles of QG-P1/QG-P2/QG-P4/QG-P8/QG-P15 TT. See QA-Tr-1.

Estimated human page views: 609