QG-P16 Schmidt Point

QG-P16 is the Involutary Conjugate (QA-Tf2) of the Miquel Point (QL-P1).

Because it is the image of a QA-Transformation wrt a QL-Point the result is a Quadrigon Point. As can be seen in the properties below it is also the image of a QL-Transformation wrt a QA-Point.

This point and most of its properties are discovered by Eckart Schmidt (November 26, 2012).

CT-Coordinates QG-P16 in 3 QA-Quadrigons

(-a² (p + q + r) (-c² p² q – c² p q² + b² p² r + a² p q r + b² p q r – 2 c² p q r + a² q² r) :

(c² p q + b² p r + a² q r) (a² p q – b² p q + a² q² – b² q² + c² q² – b² p r – b² q r + c² q r) :

-c² (p + q + r) (c² p q² – 2 a² p q r + b² p q r + c² p q r – a² q² r + b² p r² – a² q r²))

(-(c² p q + b² p r + a² q r) (a² p² – b² p² – c² p² + a² p q – b² p q + a² p r – c² p r + a² q r) :

-b² (p + q + r) (-c² p² q – c² p q² + b² p² r + a² p q r + b² p q r – 2 c² p q r + a² q² r) :

-c² (p + q + r) (c² p² q – b² p² r + a² p q r – 2 b² p q r + c² p q r – b² p r² + a² q r²))

(-a² (p + q + r) (c² p² q – b² p² r + a² p q r – 2 b² p q r + c² p q r – b² p r² + a² q r²) :

-b² (p + q + r) (c² p q² – 2 a² p q r + b² p q r + c² p q r – a² q² r + b² p r² – a² q r²) :

-(c² p q + b² p r + a² q r) (c² p q – a² p r + c² p r – b² q r + c² q r – a² r² – b² r² + c² r²))

DT-Coordinates QG-P16 in 3 QA-Quadrigons

(p²/(b² p⁴ – a² p² q² – b² p² q² + 2 c² p² q² + a² q⁴ – b² p² r² – a² q² r²) :

1/(-a² p² + b² p² + c² p² + a² q² – b² q² + c² q² + a² r² + b² r² – c² r²) :

r²/(-c² p² q² + c² q⁴ – b² p² r² + 2 a² q² r² – b² q² r² – c² q² r² + b² r⁴))

( 1/(a² p² – b² p² – c² p² – a² q² + b² q² – c² q² – a² r² – b² r² + c² r²) :

-(q²/(b² p⁴ – a² p² q² – b² p² q² + 2 c² p² q² + a² q⁴ – b² p² r² – a² q² r²)) :

-(r²/(c² p⁴ – c² p² q² – a² p² r² + 2 b² p² r² – c² p² r² – a² q² r² + a² r⁴)))

(p²/(c² p⁴ – c² p² q² – a² p² r² + 2 b² p² r² – c² p² r² – a² q² r² + a² r⁴) :

q²/(-c² p² q² + c² q⁴ – b² p² r² + 2 a² q² r² – b² q² r² – c² q² r² + b² r⁴) :

1/(-a² p² + b² p² + c² p² + a² q² – b² q² + c² q² + a² r² + b² r² – c² r²))

CT-Coordinates QG-P16 in 3 QL-Quadrigons

(-a² (l – m) m n (a² l² – a² l m – 2 b² l m + c² l m + 2 b² m² – a² l n + 2 b² l n – c² l n + a² m n – 2 b² m n – c² m n + c² n²) :

-b² l (l – m) (m – n) n (a² l – a² m – c² m + c² n) :

c² l m (m – n) (a² l² – a² l m – 2 b² l m + c² l m + 2 b² m² – a² l n + 2 b² l n – c² l n + a² m n – 2 b² m n – c² m n + c² n²))

(-a² (l – m) n (a² l² m – a² l m² – 2 b² l m² + c² l m² + 2 b² m³ – a² l² n + 2 b² l m n + a² m² n – 2 b² m² n – c² m² n – c² l n² + c² m n²) :

-l n (a² l – a² m + c² m – c² n) (b² l m – c² l m – b² m² + a² l n – b² l n + c² l n – a² m n + b² m n) :

-c² l (m – n) (a² l² m – a² l m² – 2 b² l m² + c² l m² + 2 b² m³ – a² l² n + 2 b² l m n + a² m² n – 2 b² m² n – c² m² n – c² l n² + c² m n²))

(-m (m – n) (-a² l + a² m – c² m + c² n) (a² l² – a² l m – 2 b² l m + c² l m + 2 b² m² – a² l n + b² l n + a² m n – b² m n – c² m n) :

b² (l – m) (m – n) (-a² l² m + a² l m² + 2 b² l m² – c² l m² – 2 b² m³ + a² l² n – 2 b² l m n – a² m² n + 2 b² m² n + c² m² n + c² l n² – c² m n²) :

-(l – m) m (a² l – a² m + c² m – c² n) (a² l m + b² l m – c² l m – 2 b² m² – b² l n + c² l n – a² m n + 2 b² m n + c² m n – c² n²))

DT-Coordinates QG-P16 in 3 QL-Quadrigons

(m² (m – n) (m + n) (-b² l² + c² l² + b² m² – c² n²) (a² l² – a² m² + c² m² – c² n²) :

(b² l² m² – c² l² m² – b² m⁴ – a² l³ n + a² l m² n + c² l m² n + a² l² n² – b² l² n² + c² l² n² – a² m² n² + b² m² n² – c² l n³) (b² l² m² – c² l² m² – b² m⁴ + a² l³ n – a² l m² n – c² l m² n + a² l² n² – b² l² n² + c² l² n² – a² m² n² + b² m² n² + c² l n³) :

m² (-l + m) (l + m) (-a² l² + b² m² + a² n² – b² n²) (-a² l² + a² m² – c² m² + c² n²))

(-a² (l – m) (l + m) n (b² l² m² – c² l² m² – b² m⁴ + a² l³ n – a² l m² n – c² l m² n + a² l² n² – b² l² n² + c² l² n² – a² m² n² + b² m² n² + c² l n³) :

l n (l + n) (a² l² – a² m² + c² m² – c² n²) (a² l² – a² m² – c² m² + c² n²) :

c² l (m – n) (m + n) (-b² l² m² + c² l² m² + b² m⁴ – a² l³ n + a² l m² n + c² l m² n – a² l² n² + b² l² n² – c² l² n² + a² m² n² – b² m² n² – c² l n³))

(-a² (l – m) (l + m) n (-b² l² m² + c² l² m² + b² m⁴ + a² l³ n – a² l m² n – c² l m² n – a² l² n² + b² l² n² – c² l² n² + a² m² n² – b² m² n² + c² l n³) :

-l (l – n) n (a² l² – a² m² + c² m² – c² n²) (a² l² – a² m² – c² m² + c² n²) :

c² l (m – n) (m + n) (-b² l² m² + c² l² m² + b² m⁴ + a² l³ n – a² l m² n – c² l m² n – a² l² n² + b² l² n² – c² l² n² + a² m² n² – b² m² n² + c² l n³))

Properties

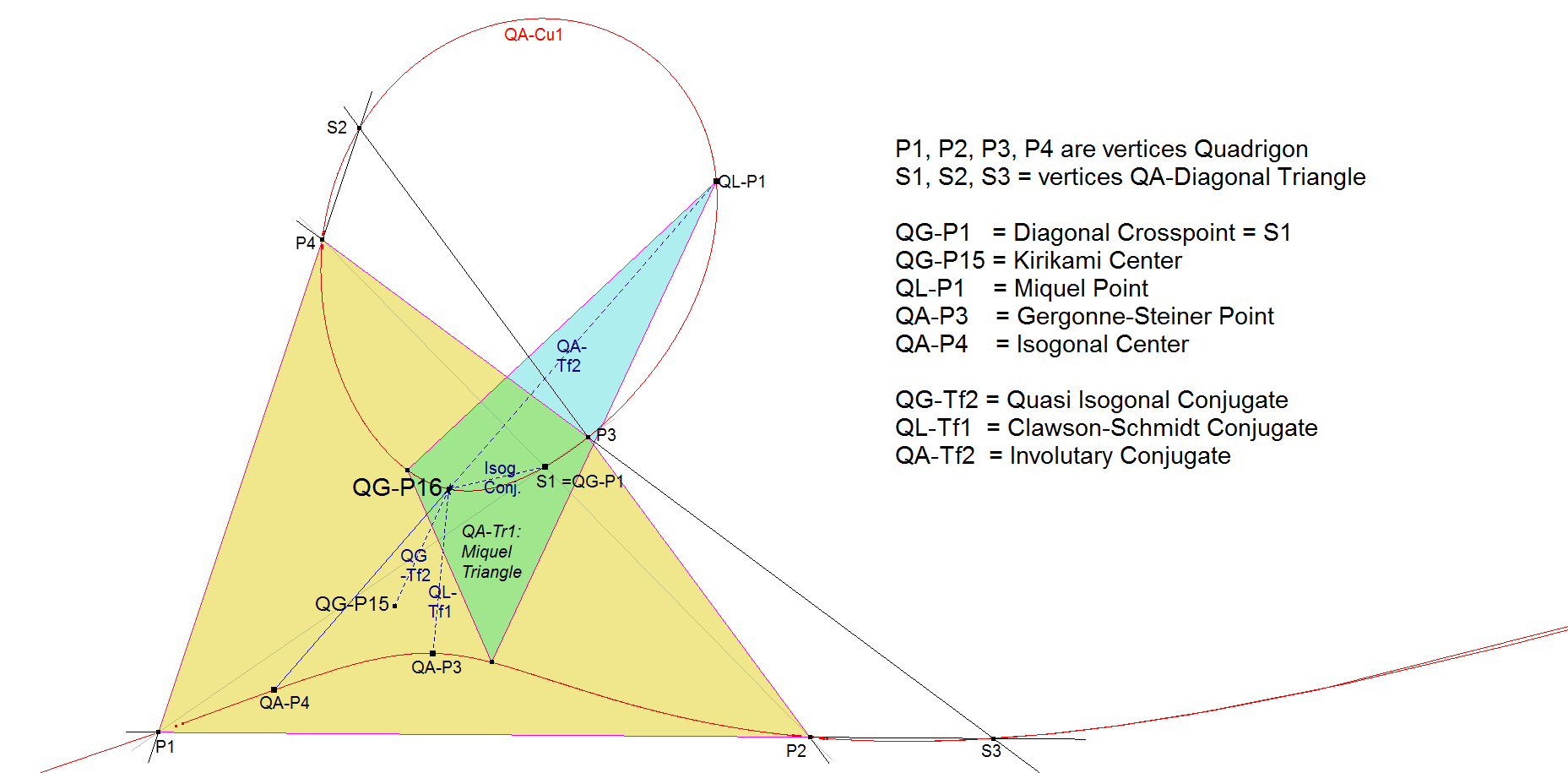
• QG-P16 is the Isogonal Conjugate of QG-P1 wrt the Miquel Triangle (QA-Tr2).
• QG-P16 is the QA-Tf2 image (Involutary Conjugate) of QL-P1.
• QG-P16 is the QL-Tf1 image (Clawson-Schmidt Conjugate) of QA-P3.
• QG-P16 is the QG-Tf2 image (Quasi Isogonal Conjugate) of QG-P15.
• QG-P16 is collinear with QL-P1, QA-P4.
• QG-P16 is the perspector of the Miquel triangle and the triangle formed by QA-P4 and the QA-Tr1-vertices unequal QG-P1.
• QG-P16.QG-P1 is parallel with QA-L4.
• QG-P16 lies on QA-Cu1 and the asymptote of QA-Cu1 is parallel to QG-P16.QG-P1.
• The three QG-P16 points of a quadrilateral are collinear on QL-L11, which is the QL-Tf1 image of the Dimidium circle QL-Ci6.
• The QA-Möbius Conjugate (QA-Tf4) of QG-P16 is a point on the line QA-P4.QG-P5.
• QG-P16 lies on the polar of QL-P1 wrt QG-Co2 (and invers) (Eckart Schmidt, October 9, 2013). See [34], QFG # 286.
• The Triple Triangle of QG-P16 is perspective with all QA-Component Triangles (see QA-Tr-1 for Desmic Triple Triangles).

Estimated human page views: 598