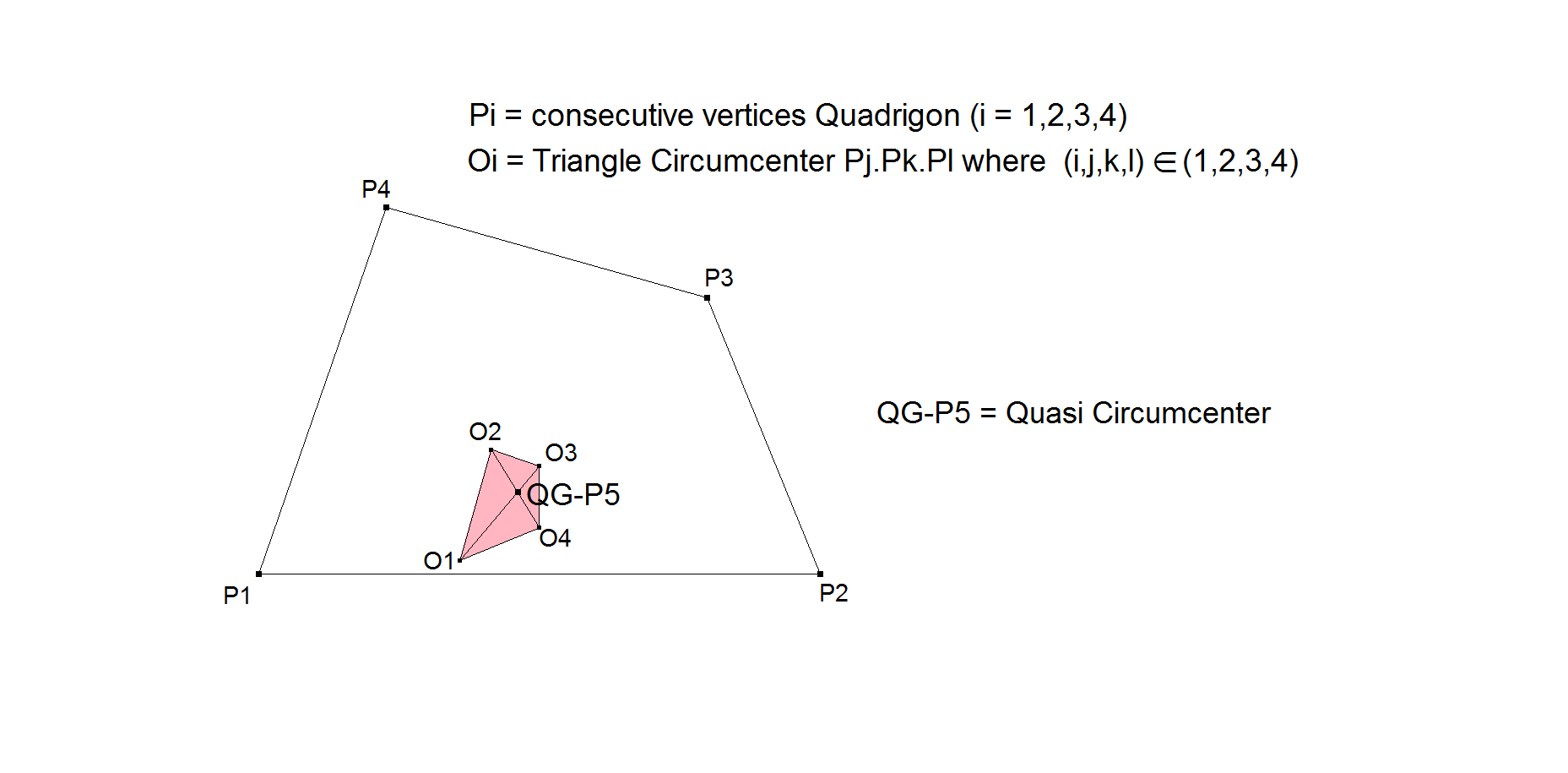
QG-P5: 1^st Quasi Circumcenter

The 1^st Quasi Circumcenter is the Diagonal Crosspoint of the X3-Quadrigon.

The X3-Quadrigon is defined by its vertices being the Triangle Circumcenters of the component triangles of the Reference Quadrigon.

This point and other 1^st quasi points are described in [5].

As can be seen in next picture, there are more special properties about this point:

CT-coordinates QG-P5 in 3 QA-Quadrigons: (only coordinates of 1^st Quadrigon point are given)

(a² S_A (p² + r²) – (a² + c²) S_C p r – (a² – c²) S_B p q – a² (a² – c²) q r + 8 Δ² p r :

b² S_B ( p² + q r + r² + p q) + a² b² r (p + q) + b² c² p (q + r) :

c² S_C (p² + r²) – (a² + c²) S_A p r + (a² – c²) S_B q r + c² (a² – c²) p q + 8 Δ² p r)

CT-coordinates QG-P5 in 3 QL-Quadrigons: (only coordinates of 1^st Quadrigon point are given)

(b² c² l m (m – n)² – c⁴ l m (m – n)² + a⁴ (l – m) (l m² + l n² – m n²) + a² (-b² (l – m) (l m² – 2 l m n + 2 m² n + l n² – m n²) + c² (-l² m² + 2 l m³ + 2 l² m n – 2 l m² n – l² n² + l m n² – m² n²)) :

-a⁴(l – m)l m n + c⁴ l m (m – n) n + b⁴(l – m) (m – n) (l m – l n + m n) – b²c²(m – n) (l² m + l m² – l² n + l m n – m² n) + a² (c² l m n (l – 2 m + n) – b² (l – m) (l m² – l m n – m² n + l n² – m n²)) :

-a⁴ (l – m)² m n + c⁴ (m – n) (l² m – l² n – m² n) – b² c² (m – n) (l² m – 2 l m² – l² n + 2 l m n – m² n) + a² (b² (l – m)² m n + c² (-l² m² + l² m n – 2 l m² n + 2 m³ n – l² n² + 2 l m n² – m² n²)))

CT-Area of QG-P5-Triangle in the QA-environment: (equals 4x area QA-Morley Triangle)

(c² p q + b² p r + a² q r)² / (8 Δ (p + q) (p + r) (q + r) (p + q + r))

CT-Area of QG-P5-Triangle in the QL-environment

((a² mn (l-m) (l-n)(lm-mn+ln) + b² nl(m-l)(m-n)(lm+mn-ln) + c² lm (n-l)(n-m)(-lm+mn+ln))²)

/(16 Δ (l – m)² (l – n)² (m – n)² (-lm+ln+mn) (lm+ln-mn) (lm-ln+mn))

–

DT-coordinates QG-P5 in 3 QA-Quadrigons: (only coordinates of 1^st Quadrigon point are given)

(2 Sb (Sa p²+Sb q²) (p²-r²)+Sc (p²-q²-r²) (Sa p²+Sc r²)+Sb Sc (p⁴-p² q²-3 q² r²-r⁴) :

Sa (Sa p²+Sb q²) (p²+q²-r²) + Sc (-p²+q²+r²) (Sb q²+Sc r²) – Sa Sc q² (p²-q²+r²) :

-2 Sb (p²-r²) (Sb q²+Sc r²)-Sa (p²+q²-r²) (Sa p²+Sc r²)-Sa Sb (p⁴+3 p² q²+q² r²-r⁴))

DT-coordinates QG-P5 in 3 QL-Quadrigons: (only coordinates of 1^st Quadrigon point are given)

(a² m² (c² n²-Sa m²-Sb l²) : m² (Sb Sc l²+Sa Sc m²+Sa Sb n²)-S² l² n² : c² m² (a² l²-Sc m²-Sb n²))

DT-Area of QG-P5-Triangle in the QA-environment: (equals 4x area QA-Morley Triangle)

-(Sa p²+Sb q²+Sc r²)² / (2 S (-p+q+r) (p+q-r) (p-q+r) (p+q+r))

DT-Area of QG-P5-Triangle in the QL-environment:

(Sc (l²-m²)² n²+Sb (l²-n²)² m²+Sa (m²-n²)² l²)² / (2 S (l²-m²)² (l²-n²)² (m²-n²)²)

Properties

• QG-P4, QG-P5, QG-P6, QG-P7 are collinear on QG-L4, the 1st QG-Quasi Euler Line.
• QG-P5 is the Reflection of QG-P1 in QG-P9 and the Reflection of QG-P6 in QG-P7.
• QG-P5 is the Reflection of QA-P24 in QL-P2 (Eckart Schmidt, July, 2012).
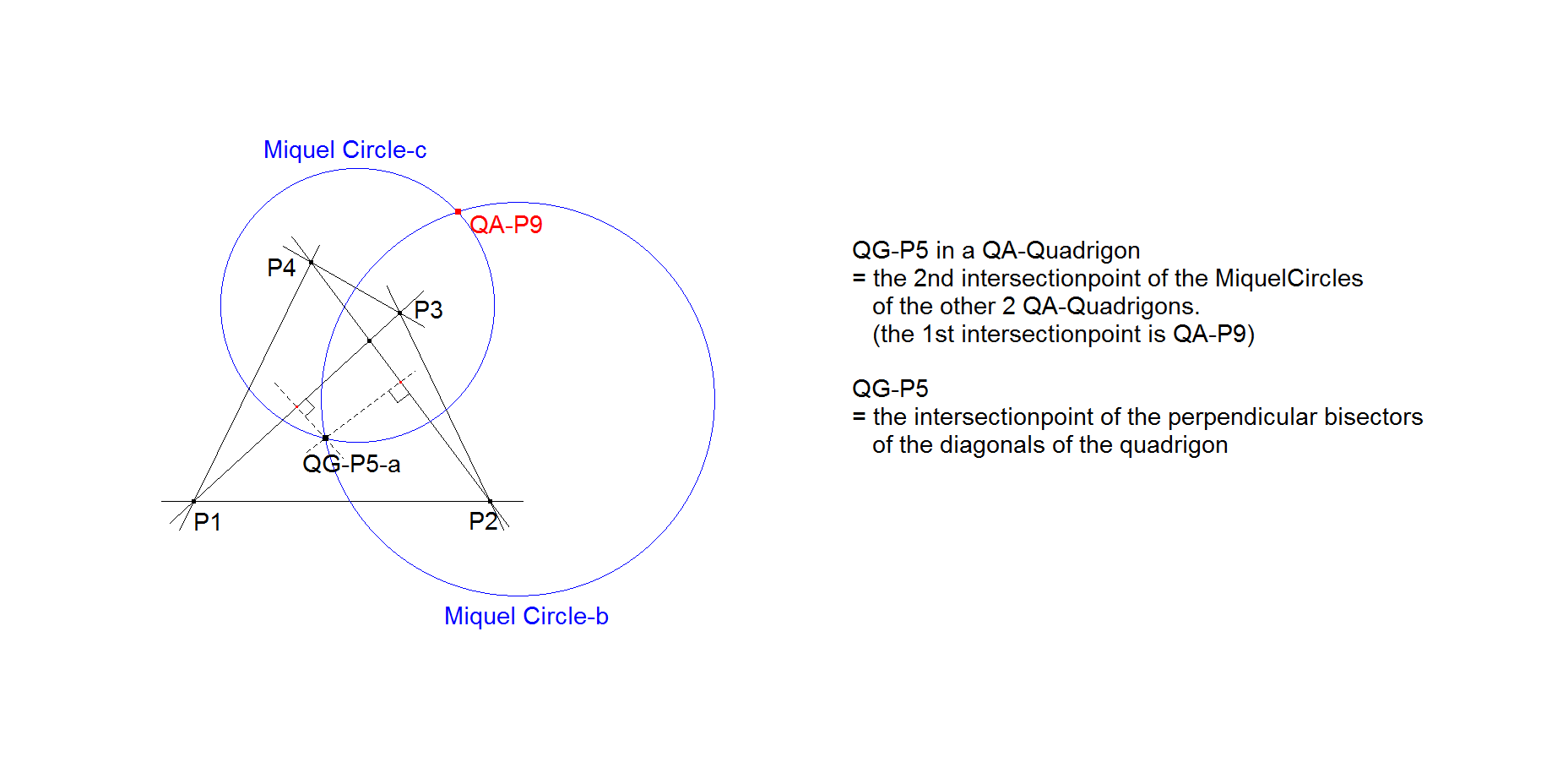
• QG-P5 is the intersection point of the perpendicular bisectors of the diagonals.
• QG-P5 is the Circumcenter of the 1^st QG-Quasi Diagonal Triangle: QG-Tr1.
• QG-P5 in a QA-Quadrigon = the 2nd intersection point of the Miquel Circles of the other 2 QA-Quadrigons (the 1st intersection point is QA-P9).
• The three QA-versions of QG-P5 lie on a circle through QA-P3, centered in the reflection of QA-P15 in QA-P1. See [34], Eckart Schmidt, QFG#1263.
• In a Quadrangle the QG-P5-Triangle is perspective with the QL-P1-Triangle (QA-Tr2). Their perspector is not registered in EQF.
• In a Quadrangle the QG-P5-Triangle is perspective and homothetic with the QL-P2-Triangle (QA-Tr3). The area of the 1^st Triangle equals 4x the area of the 2^nd Triangle. Their perspector is QA-P24.
• In a Quadrilateral the QG-P5-Triangle is perspective with both the QG-P1-Triangle (QL-Tr1) and the QG-P9-Triangle. Their common perspector is QL-P16.
• In a Quadrilateral the sides of the QG-P5-Triangle pass through the midpoints of the 3 QL-Diagonals at the Newton Line (QL-L1).
• QA-P3 (Gergonne-Steiner Point) lies on the circumcircle of the triangle formed by the 3 QA-versions of QG-P5.
• QL-P16 as well as QL-P17 lie on the circle defined by the 3 QL-versions of QG-P5 and on the circle defined by the 3 QL-versions of QG-P9. Moreover the center of the circle defined by the 3 QL-versions of QG-P5 lies on the circle defined by the 3 QL-versions of QG-P9.
• The sidelines of the triangle formed by the 3 QA-versions of QG-P5 are the loci of points P where d₁² + d_i² = d_j² + d_k² ( (i,j,k) ∈ (2,3,4) ), where d_i = distance (P, P_i).
• The QA-Orthopole (QA-Tf3) of QG-P5 is QG-P7.
• The QA-Möbius Conjugate (QA-Tf4) of QG-P5 is QL-P1.
• Let M13, M24 be the Midpoints of P1.P3 and P2.P4. Let O = QG-P5.
• Now the two angles between the lines O.M13 and O.M24 correspond with (Angle P1.O.P2 + Angle P3.O.P4)/2 and (Angle P2.O.P3 + Angle P4.O.P1) /2.
• See [34], QFG messages 417,418.
• The QG-P5 Triple Triangle in a Quadrangle is Orthologic wrt all QA-Component Triangles (Seiichi Kirikami, [34], QFG #980, # 982). See QA-Tr-1.

Estimated human page views: 556