QL-Cu1

QL-Cu1: QL-Quasi Isogonal Cubic

QL-Cu1 has several special characteristics:

QL-Cu1 is the locus of all points P for which the Isogonal Conjugates wrt all 4 component triangles coincide in a point on the same cubic. So the cubic is in terms of a quadrilateral QL-self-isogonal.
QL-Cu1 is the locus of all points P for which the QG-Quasi Isogonal Conjugates wrt all 3 component quadrigons coincide in a point on the same cubic.
QL-Cu1 is the locus of the foci of all inscribed conics in the Reference Quadrilateral.
QL-Cu1 is the locus of all points for whom the Midpoint of this point and its Clawson-Schmidt Conjugate lie on the Newton Line QL-L1.
QL-Cu1 is the locus of all points P for which the reflections of P in the 4 quadrilateral lines are concyclic (Seiichi Kirikami in [34], EQF message #1093).
QL-Cu1 is the locus of all points P for which the feet of the perpendiculars from P to the 4 quadrilateral lines are concyclic (all lie on a circle).
QL-Cu1 is the locus of points, whose Antipedal Quadrigon is cyclic (if not degenerated) (see [34] message #355 from Eckart Schmidt).
QL-Cu1 is the locus of all points P where all perpendiculars from Li^Lj at Si.Sj coincide in a point on the same cubic, where Si = pedal point of P on Li.
QL-Cu1 is the locus of points, whose reflections in the circumcircles of the QL-Component Triangles are concyclic (Eckart Schmidt in [34], EQF message #403).
If the Reference System is the Reference Quadrilateral, this cubic is a circular isocubic invariant to the Clawson-Schmidt Conjugate QL-Tf1.

If the Reference System is the Orthic Triangle of the QL-Diagonal Triangle, this cubic is an isogonal circular cubic.

This Quadrilateral Cubic is also described (with other names) by Fred Lang (see [24] page 3) and Eckart Schmidt (see [15e]).

More information about the type of cubic is described by Bernard Gibert at [17b] and [17d].

More information about the subject also can be found at [43].

How to draw a line through all 6 points of a Quadrilateral . . .

Construction

Let P be some point on QL-L2 (Steiner Line).
P* = Isogonal Conjugate of P wrt Triangle L2.L3.L4 (or any other QL-Component Triangle).
Co1= Conic through vertices triangle L2.L3.L4 and QL-P1 and P*.
Pr = P reflected in QL-L1 (Newton Line).
Lr = line through Pr // QL-L1 (now P is railway watcher).
S1 and S2 are intersection points Lr ^ Co1.

QL-Cu1 is the locus of S1and S2 with variable P on QL-L2 (Steiner Line).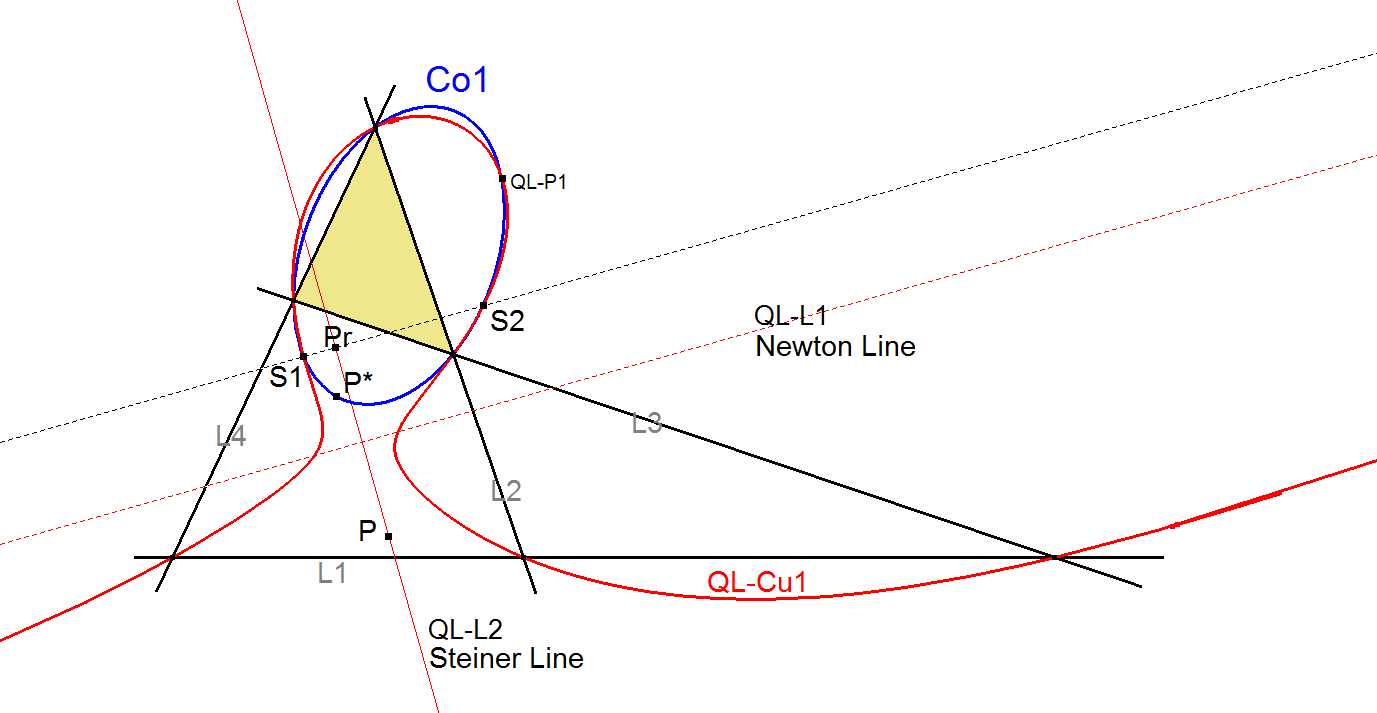 Infovisual QL-Cu1-infovisual-cvt-02.png

For other properties regarding QL-Cu1 see [34], QFG # 193 and # 194.

Conjugates on QL-Cu1

The Clawson-Schmidt Conjugate (QL-Tf1) is very important on QL-Cu1.

It is very special that this conjugate has the same performance for points on QL-Cu1as:

the Isogonal Conjugate of P wrt the Orthic Triangle of the QL-Diagonal Triangle (note Eckart Schmidt).
the Quasi Isogonal Conjugate (QG-Tf2) of P wrt any Quadrigon of the Reference Quadrilateral (note Eckart Schmidt).

Other properties of this conjugate:

Conjugated pairs of points on QL-Cu1 lie at different sides of the Newton line at equal distances.
The tangents of a pair of conjugated points on QL-Cu1 will intersect in another point at QL-Cu1 (see [34], QFG # 185).

Easy construction method of Clawson-Schmidt conjugated points on QL-Cu1

Any point X on QL-Cu1 can be seen as the intersection point of the line Ln parallel to the Newton line and the connecting line Lp=QL-P1.X.

Now CSC(X) can be constructed as the intersection point of La’ and Lb’, where:

Ln’ = Ln Reflected in the Newton Line

Lp’ = Lp reflected in the 1^st Steiner Axis (see description at QL-Tf1)

1st Steiner Axis

The 1st Steiner Axis easily can be constructed as:

an internal angle bisector of Sij.QL-P1.Skl, where Sij=Li^Lj, Skl=Lk^Ll for all (i,j,k,l) ∈ (1,2,3,4), or
the internal angle bisector if QL-2P2a.QL-P1.QL-2P2b, where QL-2P2a and QL-2P2b are the two points on the Newton Line that are mutually conjugated.

As a consequence, when X1 and X2 are CS-conjugated points, then the line through X1 parallel to QL-L1 and the line X2.QL-P1 will cross in another point on QL-Cu1. X1 and X2 can be interchanged here.

Two interesting new points on QL-Cu1

S = the intersection point of the asymptote and line QL-P1.QL-P4.
T = the intersection point of the perpendicular bisector of QL-2P2a/b and the line through QL-P1 parallel to QL-L1.
S and T are Clawson-Schmidt Conjugated,
and so the intersection point of their tangents at QL-Cu1 also lies at QL-Cu1.

Tangents to QL-Cu1

The tangent at QL-Cu1 in QL-P1 = QL-P1.QL-P4.
This line is also tangent in QL-P1 at the circle (QL-P1,QL-2P2a,QL-2P2b), which is the Clawson-Schmidt Conjugate (QL-Tf1) of the Newton Line QL-L1.
The tangent at QL-Cu1 in T is S.T reflected in the perpendicular bisector of line segment QL-2P2a.QL-2P2b.

General construction method of the tangent in a point P on QL-Cu1

(method Eckart Schmidt, see [15e] and [34], QFG # 194)

Let P* be the isogonal conjugate of P
and Co1 the isogonal conjugate of PP* wrt the triangle L1,L2,L3
and Co2 the isogonal conjugate of PP* wrt the triangle L2,L3,L4.
Let Q be the 4^th intersection of Co1 and Co 2.
Then PQ is the tangent in P wrt QL-Cu1.

Equation in CT-notation

a² l (m y + n z) y z + b² m (n z + l x) x z + c² n (l x + m y) x y + 2 (S_A m n + S_B l n + S_C l m) x y z = 0

CT-coordinates Infinity Point Asymptote

( l (m – n) : m (n – l) : n (l – m) )

Equation in DT-notation

l² x² (SA x – SB y – SC z)– m² y² (SA x – SB y + SC z) – n² z² (SA x + SB y – SC z)

– (a² l²+ b² m²+ c² n²) x y z = 0

DT-coordinates Infinity Point Asymptote

( m² – n² : n² – l² : l² – m² )

Properties

These points lie on QL-Cu1:
- all 6 intersection points of the 4 lines of the Reference Quadrilateral
- QL-P1: the Miquel Point
- QG-P17a/b/c: the vertices of the Orthic Triangle of the QL-Diagonal Triangle
- QG-P18a/b/c: the 3 QL-versions of QG-P18
- the 3 QL-versions of QG-2P5a and QG-2P5b: the intersection points of QG-Ci2 with the QG-Diagonals
- there are exactly 2 points on the Newton Line that are each other’s Isogonal Conjugate wrt all 4 QL-Component Triangles. Both points lie on QL-Cu1. See [34], QFG # 179.
- The Trilinear Poles of Li wrt triangle Lj.Lk.Ll, where (i,j,k,l) ∈ (1,2,3,4).
- the intersection point S of the asymptote and line QL-P1.QL-P4.
- the intersection point T of the perpendicular bisector of line segment QL-2P2a.QL-2P2b and the line parallel to QL-L1 through QL-P1.
- (S and T are a QL-Tf1-conjugated pair of points)
- the circular points at infinity (so the cubic is called circular, see [17c])
The tangents at the circular points at infinity meet at the Miquel Point QL – P1. This point also lies on QL-Cu1, which makes this cubic a Van Rees Cubic / Focal Cubic. See [17c].
The line QL-P1.QL-P4 is tangent at QL-Cu1 in QL-P1.
The asymptote of QL-Cu1 // QL-L1 = Newton Line.
Distance Miquel Point (QL-P1) to Asymptote is twice the distance from Miquel Point to Newton Line (Railway Watcher system, see QL-L-1).
QL-P21 lies on the asymptote of QL-Cu1.
The Clawson-Schmidt Conjugate (QL-Tf1) of some point P on the cubic is also a point on the cubic. Thus the cubic is invariant under Clawson-Schmidt-conjugation. See [15e].
The Clawson-Schmidt Conjugate (QL-Tf1) of some point P on QL-Cu1 is identical with the Isogonal Conjugate of P wrt the Orthic Triangle of the QL-Diagonal Triangle (note Eckart Schmidt).
The Clawson-Schmidt Conjugate (QL-Tf1) of some point P on QL-Cu1 is identical with the Quasi Isogonal Conjugate (QG-Tf2) of P wrt any Quadrigon of the Reference Quadrilateral (note Eckart Schmidt).
QL-Cu1 is the locus of intersection points of QG-Tf2(L) and QL-Tf1(L), where L = variable line through QG-P1 (Eckart Schmidt in [34], EQF message #224).
The circle through QL-2P2a & QL-2P2b and QL-P1 is the QL-Tf1 image of the Newton Line QL-L1 and is tangent at QL-Cu1 in QL-P1. The common tangent at QL-P1 is the line QL-P1.QL-P4.
Let X be a variable point on the Newton Line QL-L1, then the intersections of the angle bisector of QL-2P3a . X . QL-2P3b and its QL-Tf1 image (a circle through QL-P1) are points of QL-Cu1 (Eckart Schmidt in [34], EQF message #403).
Let P1P2P3P4 be a quadrigon: For points X on QL-Cu1 the centers of the circumcircles for P1XP2, P2XP3, P3XP4, P4XP1 are concyclic. (Eckart Schmidt in [34], EQF message #426).
QL-Cu1 is the locus for points whose angle bisectors wrt two opposite vertices of the Reference Quadrilateral are QL-Tf2 partners.
For any fixed point X on QL-Cu1, for any pair of variable QL-Tf1 conjugate points Y and Y’ (including obviously the opposite vertices of the QL), the direction of the bisectors of the angle YXY’ is the same (Eckart Schmidt, Bernard Keizer, see [34], QFG#1206, #1207).
Let A, B, C, QL-P1 be concyclic points on QL-Cu1, then QL-Cu1 is invariant wrt the ABC-isogonal conjugate (Eckart Schmidt [34], QFG#1399).

Estimated human page views: 966