← Previous Next →

QL-Tf2: QL-Line Isoconjugate

This Line Transformation QL-Tf2 is described by Chasles [51] paraphrased as follows:

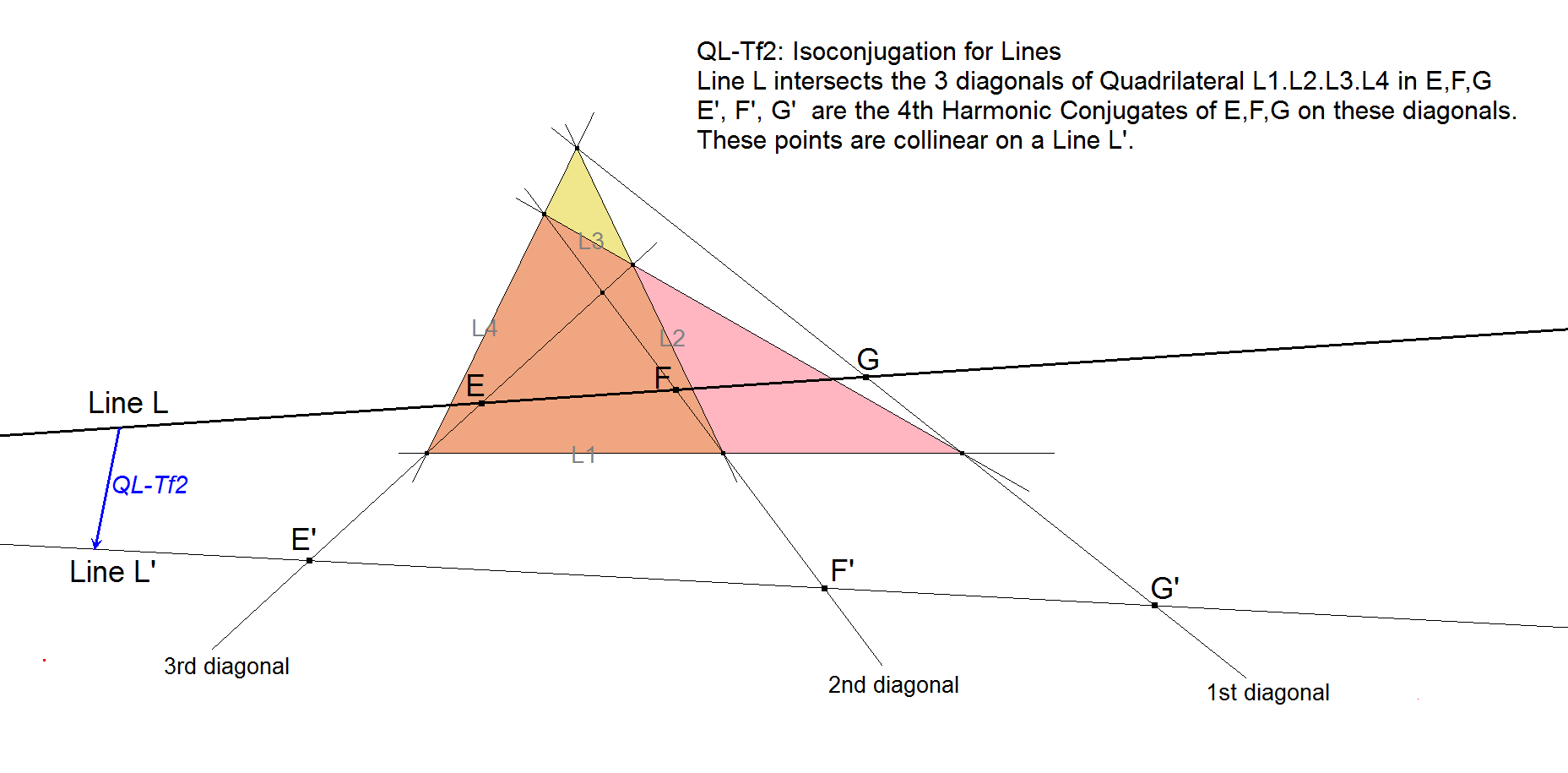
Let a line intersect the diagonals of a quadrilateral, then the 4th harmonic points on the diagonals are collinear.

The transformation QL-Tf2 is an analogue to QA-Tf2. QA-Tf2 is an Isoconjugation for Points with Reference Triangle QA-Tr1 and where the vertices of the Quadrangle are the fixed points.

According to the definition of Bernard Gibert (see [17b], 1.2.1) we can define an Isoconjugation for Lines: Reference Triangle is QL-Tr1, where the lines of the Quadrilateral are fixed lines. Considering for a line L the poles of all points wrt the inscribed triangles of the quadrilateral, there is a line as transformation of L wrt QL-Tf2.

This Line Transformation as well as its properties were further described and elaborated by Eckart Schmidt (December 16, 2012). For these and further properties see below and [34], QFG#1175.

Construction
Infovisual QL-Tf2-infovisual-cvt-01.png
CT- coefficients

L(e : f : g) -> (e (-e m n + f l n + g l m) : f (e m n – f l n + g l m): g (e m n + f l n – g l m))

DT- coefficients

L(e : f : g) -> ( f g l2 : g e m2 : e f n2 )

Properties

All not otherwise referenced properties are from Eckart Schmidt (mail December 16, 2012 and [34], messages #481, #1175).

  • QL-L1 will be transformed in the infinity line.
  • QL-L2 will be transformed in a parallel to QL-P3.QL-P4 through QL-P1.
  • For a Quadrigon the QL-Tf2 transformation of QG-P2.QG-P13 will be the reflection of QG-L1 in QG-P1.
  • The Steiner Axes (described at QL-Tf1) are QL-Tf2 partners.
  • The QL-Tf2 images of lines through a fixed point envelope an inscribed conic of the QL-Diagonal Triangle QL-Tr1. For QL-P13 we get the inscribed Steiner Elli[se of QL-Tr1. For points on the Newton line these conics are inscribed parabolas of QL-Tr1. For the Miquel Point QL-P1 we get a special inscribed conic which contacts the Steiner Axes (described at QL-Tf1) and the line QL-L2 (see [34], QFG#481).
  • The intersections of lines through a fixed point Q and their QL-Tf2 images give a cubic through the six vertices of the reference Quadrilateral as well as the vertices of the Ceva Triangle of Q wrt QL-Tr1.
  • QL-Cu1 is the locus for points whose angle bisectors wrt two opposite vertices of the Reference Quadrilateral are QL-Tf2 partners.
  • The intersections for QL-Tf2 images of perpendicular lines of a pencil are collinear.
  • QL-Tf2(L)=Tripolar(QA-Tf2h(Tripole(L))), where QA-Tf2h=QA-Tf2 wrt the Quadrangle formed by the QL-Tr1-trilinear poles of the QL-defining lines (See [34], QFG#1497,#1506 by Eckart Schmidt).
  • The QL-Tf2-image of the QL-Co1-polar of a point P contains P. See [34], Eckart Schmidt, QFG-message #1666.
  • QL-Tf2(L) is the line with the three collinear points QA-Tf7(L). See [34], Eckart Schmidt, QFG-message #2179.


Estimated human page views: 589

Scroll naar boven