nL-1: Notes on nL-objects
Many general objects in an n-Line are described by Prof. Frank Morley in the period 1886-1930.
Morley’s discoveries were all made purely by algebraic approaches. In his time it even wasn’t possible to check his discoveries in drawings because of the complicated recursive character.
His documents are often hard to understand in detail. However involved documents were piece by piece “decoded” at the end of 2014 by Bernard Keizer, Eckart Schmidt and the author of this encyclopedia in a discussion at the Yahoo Quadri-Figures Group ([34]). See especially messages #826-#917. Accordingly they are mentioned in EPG and completed with drawings using Cabri or Mathematica software.
For a quick insight pictures of n-Lines often are represented by figures bounded by n line-segments.
How many (n-1)-lines can be made up from an n-Line?
Many of the recursive constructions are based upon the property that from an n-Line exactly n different (n-1)-Lines can be made up. This can easily be deduced by omitting one line from the n-Line. This will leave behind an (n-1)-Line. Since exactly n Lines can be omitted there will be n different (n-1)-Lines contained in an n-Line. The (n-1)-Lines in an n-Line will be called the Component (n-1)-Lines. The remaining line after choosing an (n-1)-Line in an n-Line will be called the omitted line.
In descriptions we say “an n-Line contains n (n-1)-Lines” or “an n-Line has n Component (n-1)-Lines”. When we want to indicate different objects occurring in (n-1)-Lines we say that there are n versions of these (n-1)L-objects.
The n versions of an object often will be noted with a suffix consisting of un underscore and a number 1, …, n, indicating the number of the omitted line. For example a 5-Line contains 5 4-Lines and therefore has 5 4L-MVP-Centroids (4L-n-P8). They will be noted as 4L-n-P8_1, 4L-n-P8_2, 4L-n-P8_3, 4L-n-P8_4 and 4L-n-P8_5. The suffix number at the end is the number of the omitted line.
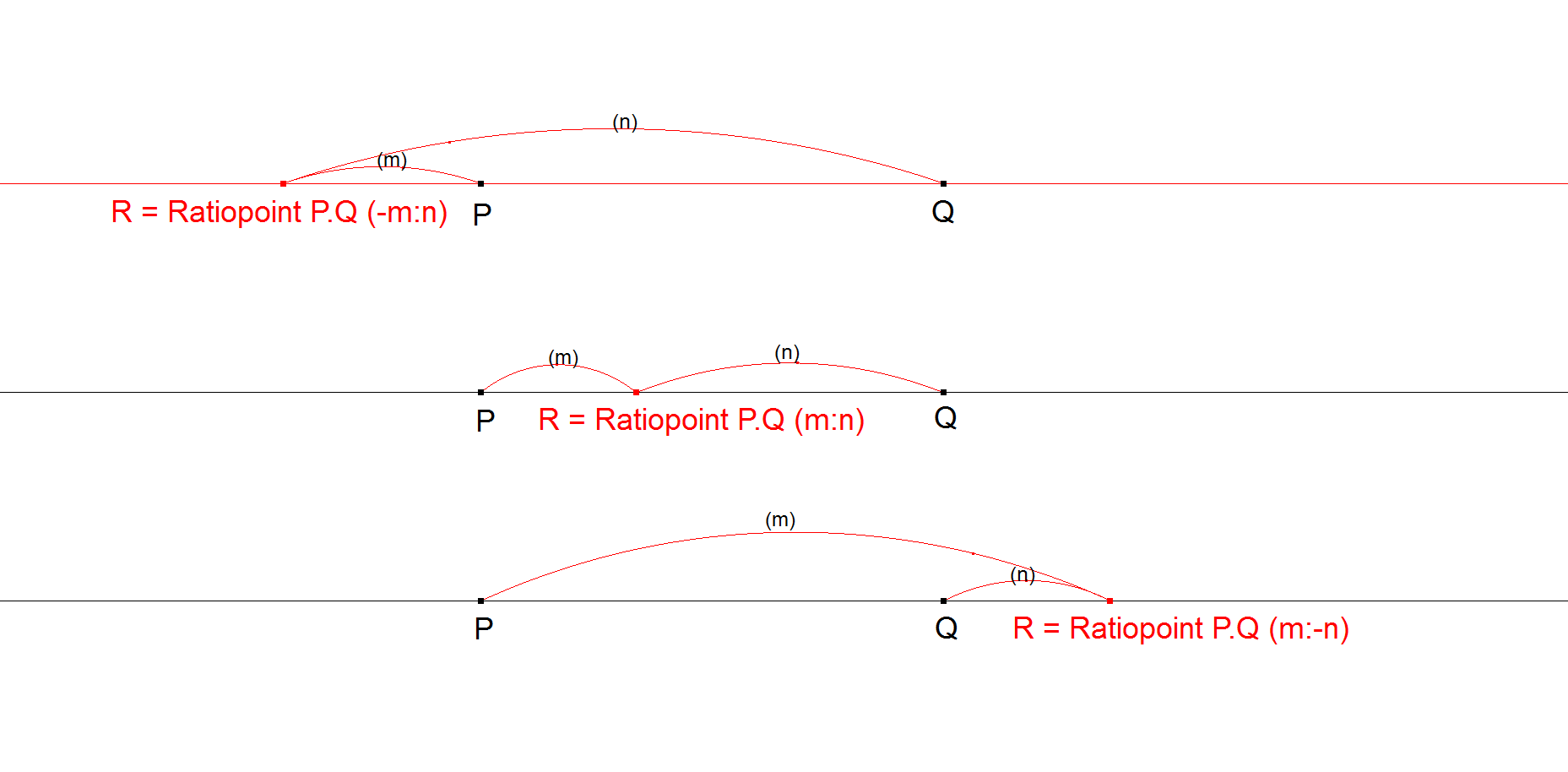
Ratiopoint
A Ratiopoint R is a point collinear to two other given points X,Y and with the distances to these two other points in a given ratio.
This method is for example used for nL-n-P5, nL-n-P7, nL-n-pi.
Recursive Eulerline situated points in an n-Line
There are different ways of construction of Eulerline points to a higher n-Line level.
All methods are based upon the central property that from any n-Line n versions of (n-1)-Lines can be constructed.
Triangle points are X(2)=Centroid, X3=Circumcenter, X(4)=Orthocenter, X(5)=Nine-point Center.
Morley’s points
| 3L-Point | 4L-Point | 5L-Point | 6L-Point | nL-Point |
|---|---|---|---|---|
| X(2) | QL-P22 | 5L-n-P2 | 6L-n-P2 | Etc. |
| X(3) | QL-P4 | 5L-n-P3 | 6L-n-P3 | Etc. |
| X(4) | QL-P2 | 5L-n-P4 | 6L-n-P4 | Etc. |
| X(5) | QL-P30 | 5L-n-P5 | 6L-n-P5 | Etc. |
Distance ratios for Morley’s Eulerline points are not preserved at the different n-levels.
MVP Points: Multi Vector Points
| 3L-Point | 4L-Point | 5L-Point | 6L-Point | nL-Point |
|---|---|---|---|---|
| X(2) | 4L-n-P8 = QL-P12 | 5L-n-P8 | 6L-n-P8 | Etc. |
| X(3) | 4L-n-P9 = QL-P6 | 5L-n-P9 | 6L-n-P9 | Etc. |
| X(4) | 4L-n-P10 = QL-P2 | 5L-n-P10 | 6L-n-P10 | Etc. |
| X(5) | 4L-n-P11 = Midpoint (QL-P2,QL-P6) | 5L-n-P11 | 6L-n-P11 | Etc. |
Distance ratios for MVP Eulerline points are preserved at the different n-levels.
Estimated human page views: 330
