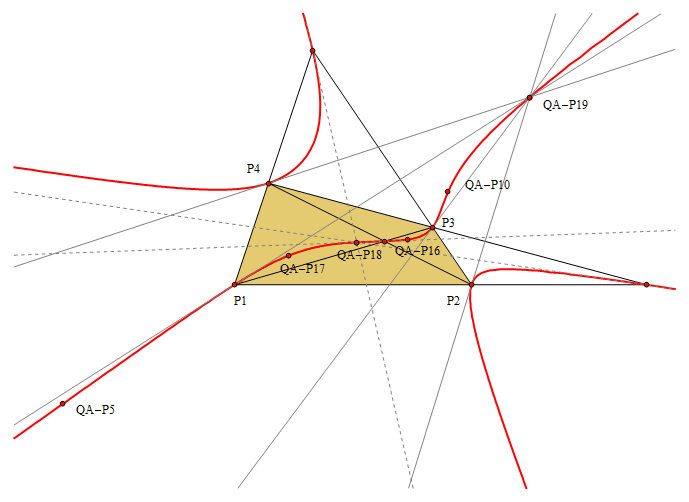
QA-Cu4: QA-DT-P19 Cubic
QA-Cu4 is the locus of the Doublepoints created by the QA-Line Involution (QA-Tf1) of all lines through QA-P19. It is a pivotal isocubic of the QA-Diagonal Triangle, invariant wrt the Involutary Conjugate with pivot QA-P19.
QA-Cu4 is a pK(QA-P16,QA-P19) cubic wrt the QA-Diagonal Triangle in the terminology of Bernard Gibert (see [17b]). (note Eckart Schmidt)
Equation CT-notation:
r2 (p+q) (p+q+2r) (p2 + q2) (q x – p y) x y
+ q2 (p+r) (p+2q+r) (p2 + r2) (p z – r x) x z
+ p2 (q+r) (2p+q+r) (q2 + r2) (r y – q z) y z = 0
Equation DT-notation:
(-p2+q2+r2)(r2 y2-q2 z2)x +(p2-q2+r2)(-r2 x2+p2 z2)y + (p2+q2-r2) (q2 x2-p2 y2) z = 0
Properties
- The vertices of the Reference Quadrangle and the QA-Diagonal Triangle lie on this cubic.
- The Involutary Conjugate pairs (QA-P5, QA-P17), (QA-P10, QA-P16) and (QA-P18, QA-P19) lie on the cubic.
- The intersection point QA-P1.QA-P31 ^ QA-P16.QA-P18 also lies on QA-Cu4.
- The intersection point QG-P1.QA-P19 ^ QG-P2.QG-P3 ^ QG-P14.QA-P5 also lies on QA-Cu4.
- The tangents at P1, P2, P3, P4 meet at QA-P19.
- The tangents at S1, S2, S3 and QA-P19 meet at QA-P18 which is the Involutary Conjugate of QA-P19 on the cubic.
Estimated human page views: 646
