QA-Tf2: Involutary Conjugate
The Involutary Conjugate of a point Q is the 2nd Doublepoint of the QA-Line Involution (see QA-Tf1) occurring on the tangent at Q to the conic (P1, P2, P3, P4, Q).
It is a conjugate because applying two times this transformation ends up in the original point.
QA-Tf2 in a Quadrangle is the equivalent of QL-Tf2 in a Quadrilateral.
The Involutary Conjugate can also be seen as the Pi-Ceva Conjugate of Q wrt Component Triangle Pj.Pk.Pl (for all combinations of (i,j,k,l) ∈ (1,2,3,4)) (note Bernard Gibert).
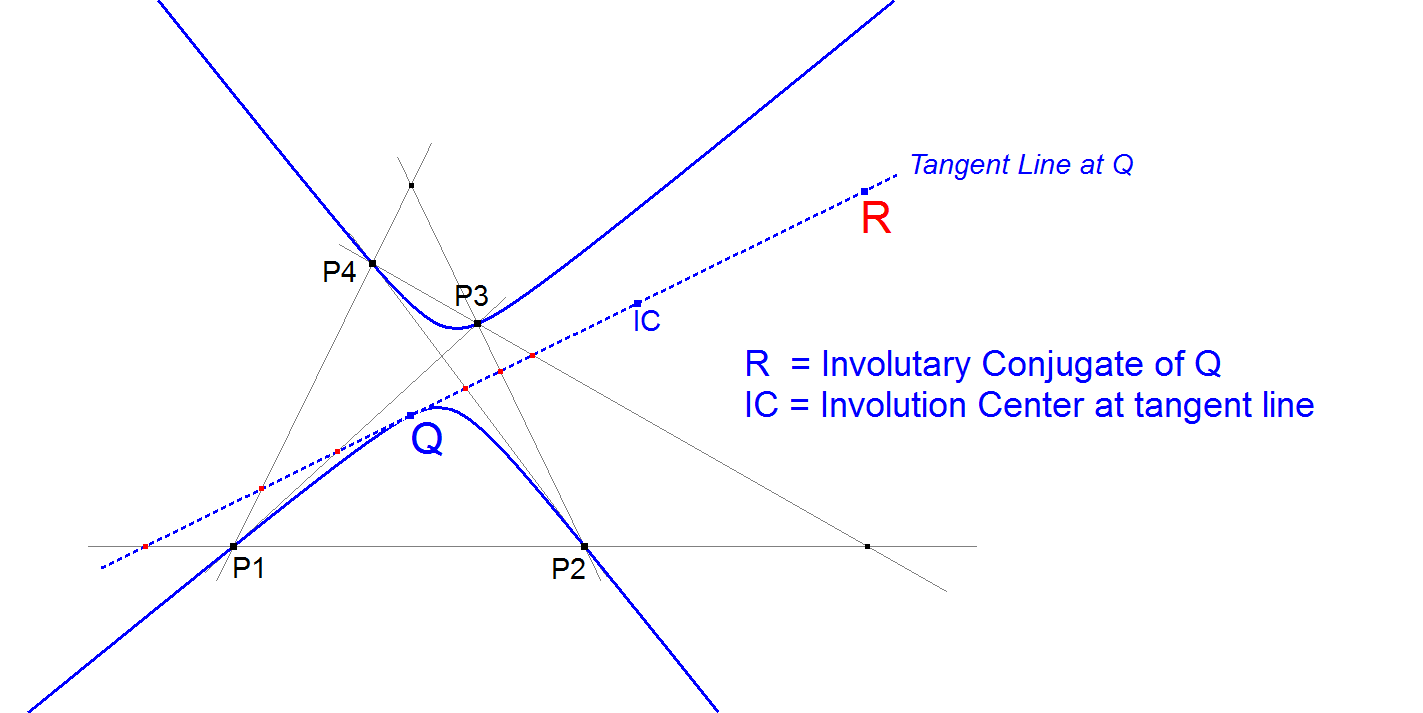
Construction 1
Construct the conic through P1, P2, P3, P4, Q.
Construct the tangent Lq at Q to this conic.
Construct the Involution Center IC of the created QA-Line Involution for Lq (see [19] as well as QA-Tf5).
Now R = the Involutary Conjugate of Q = the Reflection of Q in IC.
Construction 2
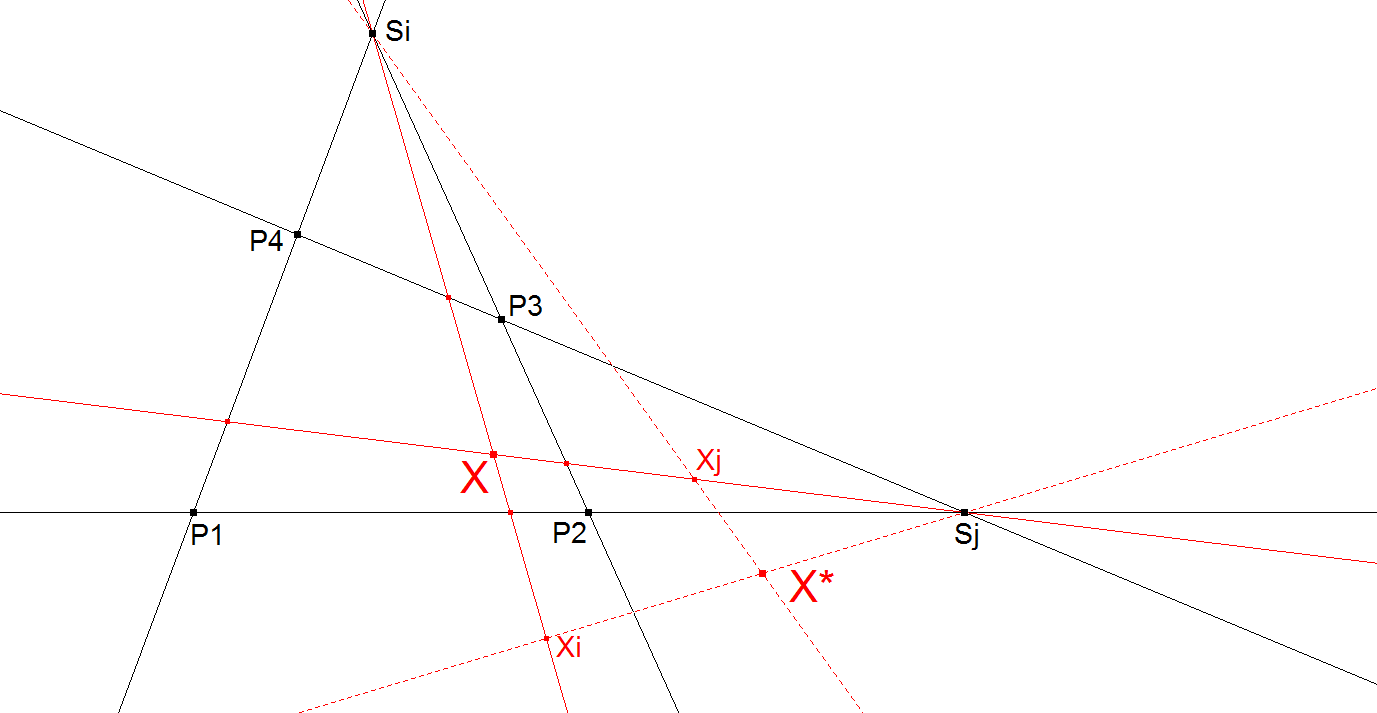
This construction is from Eckart Schmidt.
Choose one of the Component Quadrigons of the Reference Quadrangle.
Let Si and Sj be the intersection points of the opposite sides of the Quadrigon.
Connect X (the point to be transformed) with Si and Sj and construct on these lines the 4th harmonic points Xi and Xj wrt the intersection points with the crossing opposite quadrigon lines.
Connecting lines Si.Xj and Sj.Xi intersect in X*, the Involutary Conjugate of X.
Construction 3
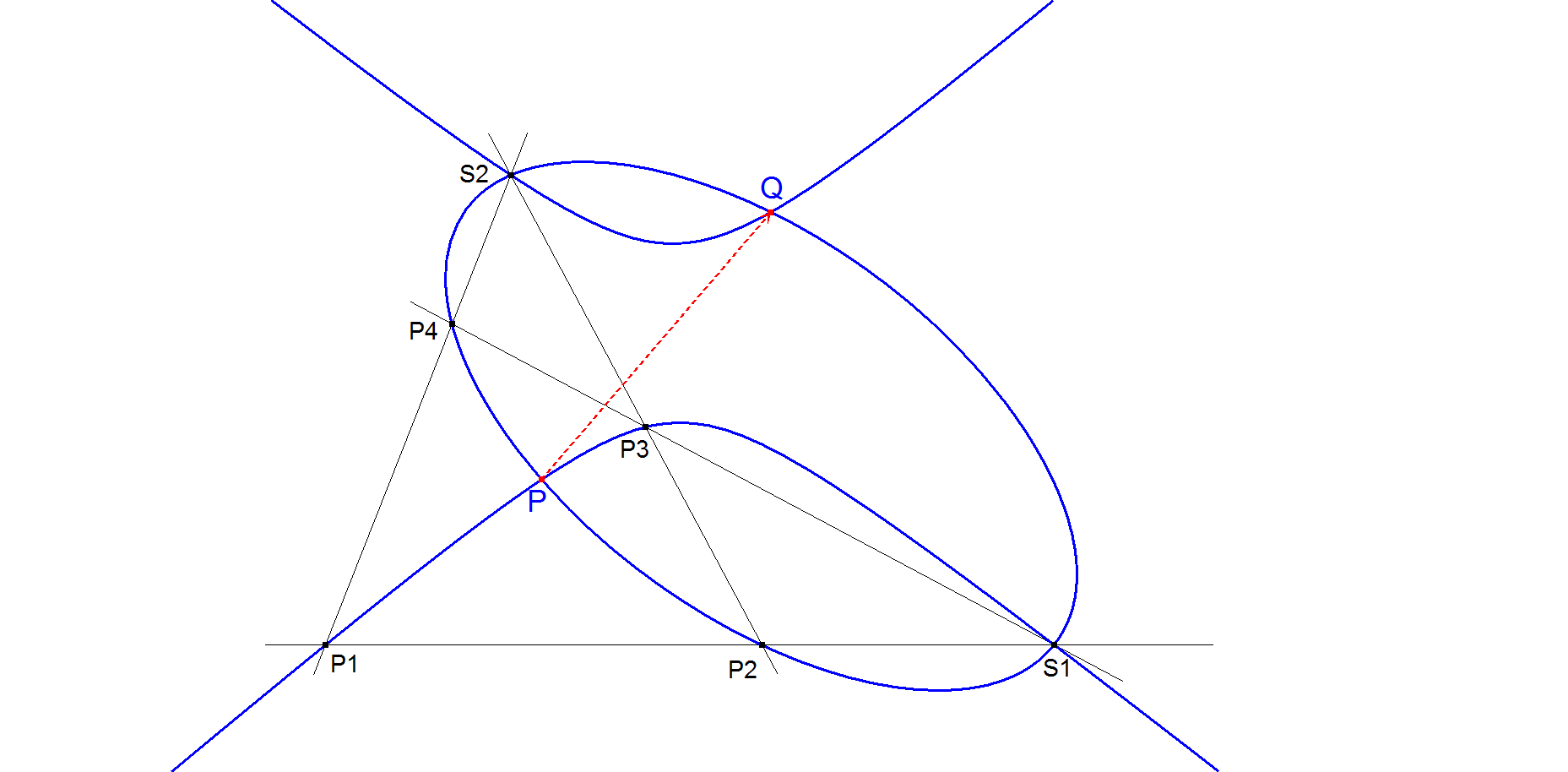
This construction is from Seiichi Kirikami. See [34], QFG messages #1491, 1492.
Let S1 = P1.P2 ^ P3.P4, S2 = P1.P4 ^ P2.P3, P is a random point.
QA-Tf2(P) = 4th intersection point of conics (P1,P3,S1,S2,P) and (P2,P4,S1,S2,P).
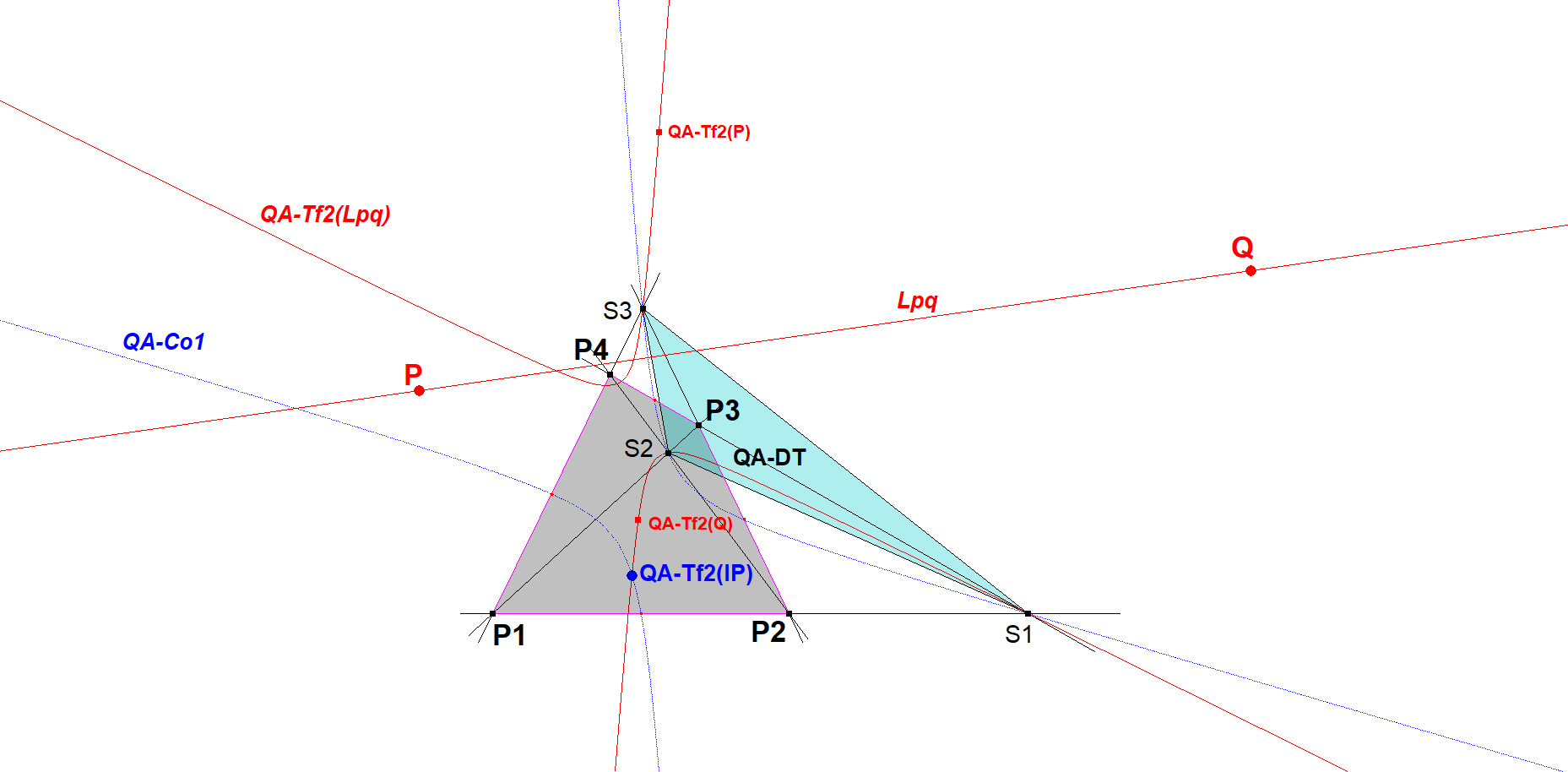
Construction of the Involutary Conjugate of the Infinity Point of some line PQ
The involutary conjugate of the infinity point of some line Lpq through P and Q will lie on the involutary conjugate of the whole line, which is a QA-DT-conic through QA-Tf2(P) and QA-Tf2(Q), here called QA-Tf2(Lpq).
Well known is that the locus of involutary conjugates of all infinity points is the nine-point conic QA-Co1. Therefore the involutary conjugate of the infinity point of some line P.Q is the 4th intersection point of QA-Co1 and QA-Cox. The other three intersection points are the vertices of the QA-Diagonal Triangle QA-DT.
Coordinates and Coefficients
Let Q (u:v:w) be a random point.
Coordinates of QA-Tf2(Q) in CT-notation
( u (q r u – p r v – p q w) : v (-q r u + p r v – p q w) : w (-q r u – p r v + p q w) )
Coordinates of QA-Tf2(Q) in DT-notation
(p2 v w : q2 w u : r2 u v)
Properties
- QA-Tf2(P)=DT-Tripole(QL-Tf2h(DT-Tripolar(P))), where QL-Tf2h=QL-Tf2 wrt the Quadrilateral formed by the QA-Tr1-trilinear polars of the QA-vertices (See QA-8 and [34], QFG#1497,#1506 by Eckart Schmidt).
- QA-Tf2(P) is the common point of the three versions of QL-Tf6(P). See [34], Eckart Schmidt, QFG#2179.
- QA-Tf2 is an isoconjugation of the diagonal triangle QA-Tr1with fixed points in the vertices of the quadrangle. See [34], Eckart Schmidt, QFG#2875.
- QA-Tf2(X) is the common point for polars of X wrt circumconics of the quadrangle. See [34], Eckart Schmidt, QFG#2855, #2856, #2875.
- Let Si (i=1,2,3) be the vertices of the QA-Diagonal Triangle and Li be the corresponding sidelines of the QA-Diagonal Triangle. QA-Tf2(P) is the common intersection point of the 4th harmonic lines of P.Si wrt (Lj,Lk), where i,j,k are different indices from (1,2,3). See [34], Bernard Keizer, QFG2878.
Examples of Involutary Conjugates
The following tables lists a number of Involutary Conjugates.
Involutary Conjugated Pairs of Points
| Point-1 | Point-2 |
|---|---|
| QA-P1: QA-Centroid | QA-P20: Reflection of QA-P5 in QA-P1 |
| QA-P4: Isogonal Center | QA-P41: Involutary Conjugate of QA-P4 |
| QA-P5: Isotomic Center | QA-P17: Involutary Conjugate of QA-P5 |
| QA-P6: Parabola Axes Crosspoint | QA-P30: Reflection of QA-P2 in QA-P11 |
| QA-P10: Centroid QA-Diagonal Triangle | QA-P16: QA-Harmonic Center |
| QA-P12: Orthocenter QA-Diag. Triangle | QA-P23: Inscribed Square Axes Crosspoint |
| QA-P18: Involutary Conjugate of QA-P19 | QA-P19: AntiCompl. of QA-P16 wrt QA-DT |
| QA-P21: Reflection of QA-P16 in QA-P1 | QA-P27: M3D Center |
Involutary Conjugates of Quadrigon Points
| Point-1 | Point-2 |
|---|---|
| QG-P12: Inscribed Harmonic Conic Center | Reflection of QG-P1 in QG-P2 |
| QG-P13: Circumscr. Harmonic Conic Center | Infinity Point of the line QG-P1.QG-P2 |
| QG-P14: Center of the M3D Hyperbola | Infinity Point of the line QG-P1.QG-P3 |
| QG-P15: Kirikami Center | Infinity Point of Newton Line |
| QG-P16: Schmidt Point | QL-P1: Miquel Point |
| QG-P18: Quasi Isogonal Crosspoint | QG-P19: Quasi Isogonal Conjugate of QG-P1 |
Involutary Conjugates of QA-Lines and QA-Curves
The Involutary Conjugate transforms lines into circumscribed conics of the QA-Diagonal Triangle. A “5th Point tangent” (see QA-Tf9) at Q is transformed into a circumscribed conic of the QA-Diagonal Triangle through Q and its Involutary Conjugate.
| QA-Line | QA-DT-Conic |
|---|---|
| Line at Infinity | QA-Co1: Nine-point Conic |
| QA-L9: Perp.Bisector QA-P2.QA-P4 | QA-Ci1: Circumcircle Diagonal Triangle |
| QA-L3: QA-Centroids Line | QA-Co5: Circumscribed DT-Conic through vertices |
| Diagonal Triangle and QA-P1, P16, P17, P19, P20 | |
| QA-L4: QA-P1.QA-P6 Line | QA-Co4: Orthogonal circumscribed DT-hyperbola |
| through vertices Diag.Tr. and QA-P3, P12, P20, P30 | |
| Line QA-P5.QA-P17.QA-P19.QA-P21 | QA-DT-Conic through QA-P5, QA-P17, QA-P18, QA-P27 |
Self-involutary Cubics
| QA-Curve | Comment |
|---|---|
| QA-Cu1 till QA-Cu5: QA-DT Cubics | self-involutary cubic |
| QA-Cu7: QA-Quasi Isogonal Cubic | self-involutary cubic |
Estimated human page views: 943
